以下分析是当改变灭弧栅片数n时，样机限流特性的变化。......
2023-06-15
开断特性仿真分析
【摘要】：图8-3为额定电流为16A的微型断路器，当短路电流通过瞬动电磁铁线圈时，铁心向左移动，顶动脱扣杆，使机构脱扣。图8-3 微型断路器现对上述微型断路器描述其仿真过程。为了验证计算准确性，在预期电流Ip=10.2kA，U=232V，cosφ=0°，βv=4.5257×10-7条件下进行了开断试验，试验结果与计算机仿真进行了对比，如图8-7所示。
图8-3为额定电流为16A的微型断路器，当短路电流通过瞬动电磁铁线圈时，铁心向左移动，顶动脱扣杆，使机构脱扣。动触头在分断弹簧作用下绕轴转动，当触头刚打开时，电弧有一个停滞过程，然后在电动力作用下，电弧由动触头转移到导弧板，并在吹弧线圈产生的磁场作用下使电弧在陶瓷隔弧片形成的缝中快速移动，进入灭弧栅片而熄灭。
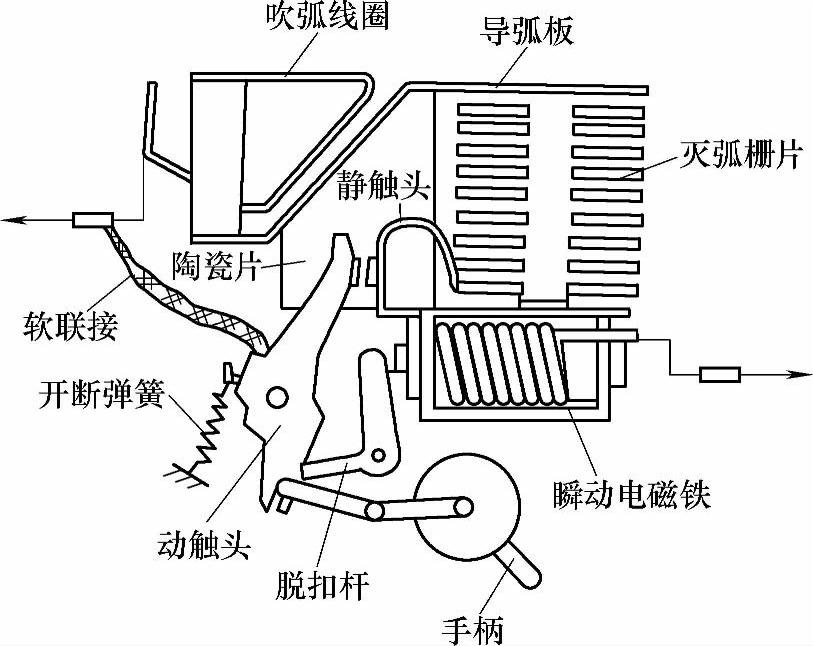
图8-3 微型断路器
现对上述微型断路器描述其仿真过程。
1.瞬动电磁铁动作过程
微型断路器动态特牲计算和前述第4章的磁脱扣器动特牲计算相似，首先用磁路或磁场方法计算并求得不同工作气隙δ和不同线圈安匣iN下瞬动电磁铁的静态吸力特性F=f（δ，iN），如图8-4所示。瞬动电磁铁的反力特性由反作用弹簧产生，如图8-5所示，其初始反力为f0=2.94N。
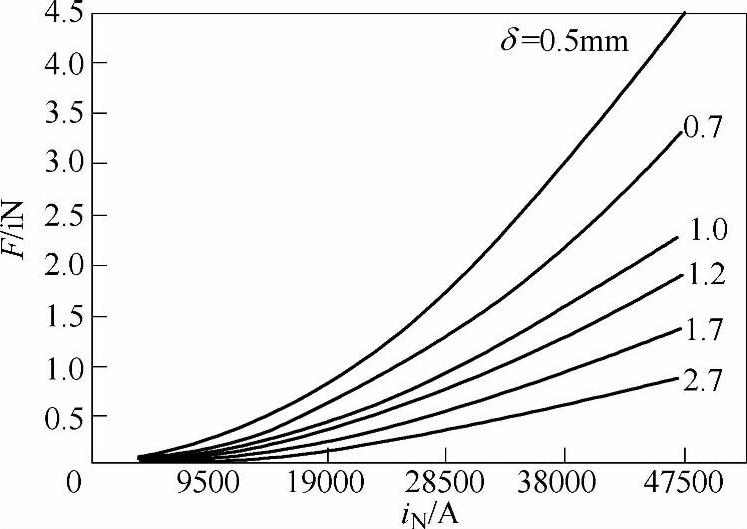
图8-4 瞬动电磁铁的吸力特性F=f（δ，iN）
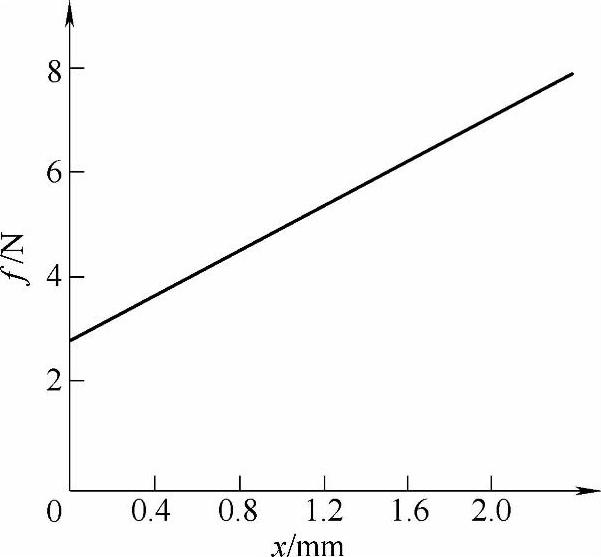
图8-5 瞬动电磁铁反力特性
式（8-1）中Uarcm，根据每一时间步长计算电流i，并在图8-4中δ=δ0的F=f（iN）曲线上，用插值法求得F，计算进行到
F-f0-fm≥ε （8-10）
则停止。上式中f0为电磁铁初始反力，fm为摩擦力，ε为判断收敛的一个小数。这一过程计算结束时，t=tc即为电磁铁触动时间，对应的电流i=ic为触动电流。
从t=tc开始，电磁铁铁心开始运动，铁心运动方程为
式中m为动铁心质量，f和fm分别为反力和摩擦力，v和x分别为铁心运动速度和行程。电路微分方程仍为式（8-1），Uarc=0，初始条件i|t=tc=ic，用数值方法求解式（8-11）时，吸力F为电流i和铁心行程x的函数，而反力f根据瞬动电磁铁的反力特性确定。上述计算当铁心行程x=d=0.8mm时，机构脱扣，铁心运动阶段结束，此时t=td，i=id。
2.电弧停滞阶段
取电弧极限长度xcrit=2mm，从动触头开始运动至电弧拉长到极限长度xcrit为止，这一阶段称为电弧停滞阶段。这一阶段电弧虽已产生，但并不运动，其电弧电压Uarc等于极间压降，这里取ΔU=23V。这一阶段使动触头部分发生转动的力矩已是动触头上拉力弹簧产生的转矩（见图8-6）加上触头间电动斥力产生的转矩。
电动斥力Fd用下式计算：
Fd=ki2（ 8-12）
式中 k——为一常数，由触头系统结构决定。k值可用计算或试验求得，对样机的k值，
k=5.793×10-7。这里Fd的单位为N。动静触头间的开断距离决定于动触头部分的运动方程，可写为
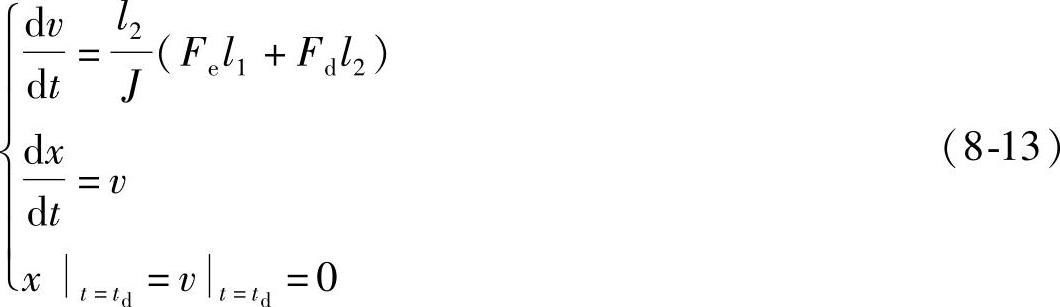
式中 v、x——分别为动触头打开速度和打开距离；
l1、l2——分别为拉力弹簧和电动斥力的力臂，如图8-6所示；
J——动触头杆的转动惯量；
Fe、Fd——分别为拉力弹簧作用力和电动斥力。
这一阶段电路方程根据式（8-1）为
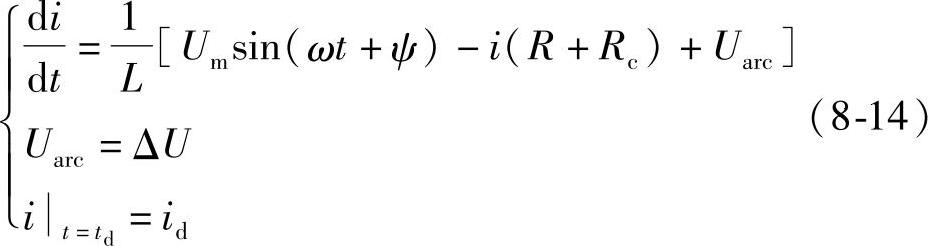
当触头之间开距x=xcrit时，这一阶段结束，此时t=ts，i=is。
3.电弧运动阶段
经过停滞阶段后，电弧开始迅速从动触头转移到导弧板，并在磁吹线圈产生的磁场作用下，向灭弧栅片运动。
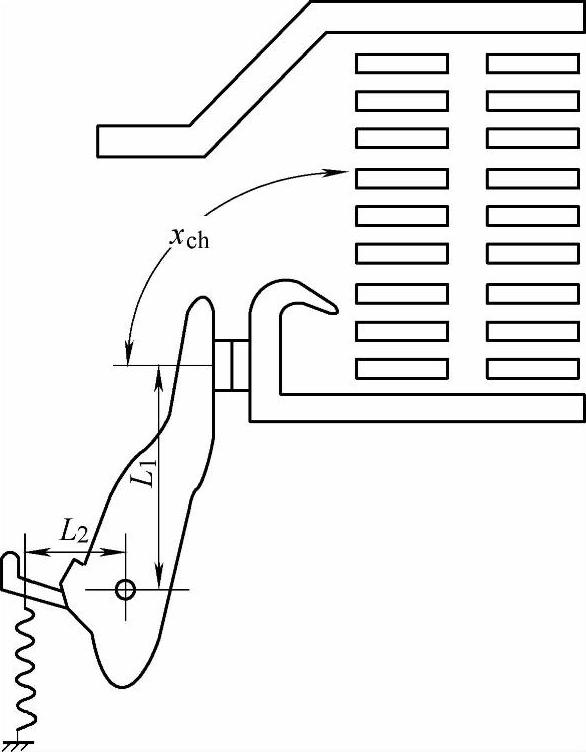
图8-6 作用在动触头上的力矩
综合式（8-6）、（8-7）和电路方程（8-1）可写出描述这一阶段的微分方程组：
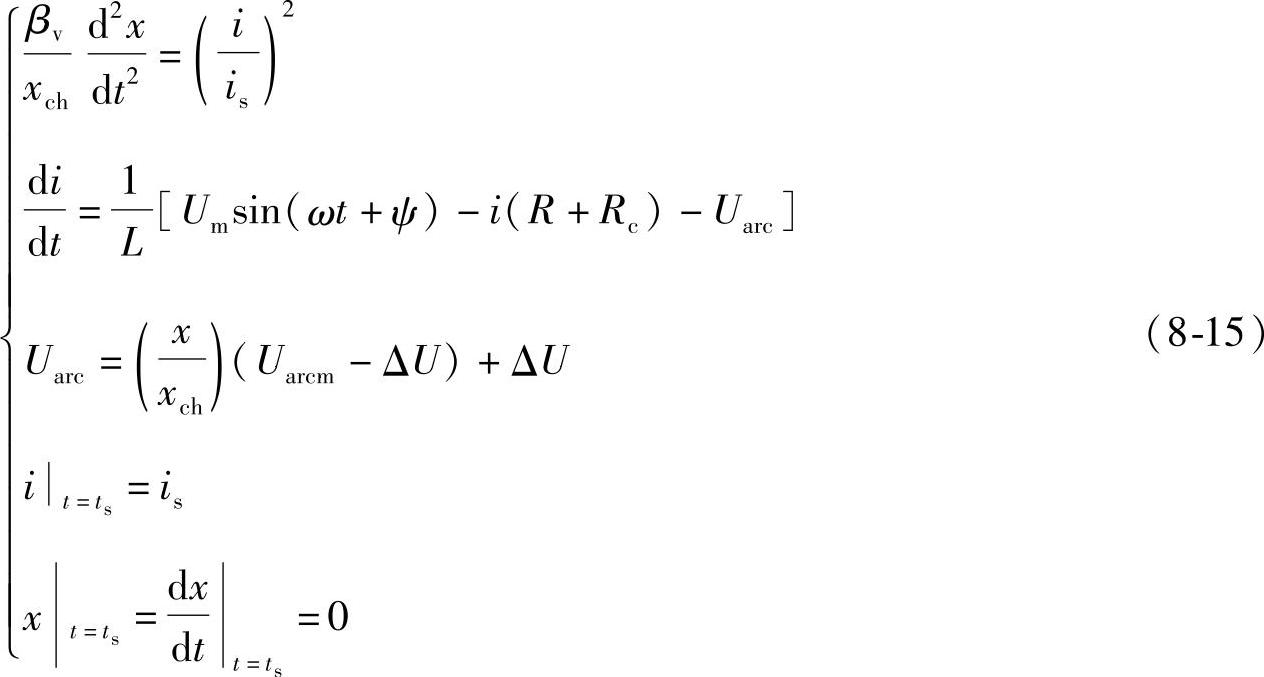
这里x为电弧运动位移，电弧到达栅片入口处的距离xch如图8-6所示，常数βv按样机开断试验的数据和波形由式（8-9）计算。根据对样机所做的开断试验波形，在预期短路电流为14.4kA，U=232V，cosφ=0.4，合闸相角ψ=0°条件下，测得is=2796.54A，ts=1.9ms。在ts～thd时间内，再利用试验测得的波形i=f（t）上的数据，按公式（8-9）用数值积分求得βv=4.5257×10-7。当电弧运动位移达x=xch=23.42mm，电弧运动阶段结束，此瞬间t=thd，i=ihd。
4.熄弧阶段
电弧进入灭弧栅片后，依靠灭弧栅片把电弧分割成许多短弧而使电弧熄灭，此时电弧电压达到峰值Uarcm，按式（8-8）计算其值。该阶段仅需求解电路微分方程式（8-1），取初始条件i|t=thd=ihd即可，这一过程进行到i=0即电弧熄灭。
为了验证计算准确性，在预期电流Ip=10.2kA，U=232V，cosφ=0°，βv=4.5257×10-7条件下进行了开断试验，试验结果与计算机仿真进行了对比，如图8-7所示。对比结果，说明仿真已满足工程实用需要。
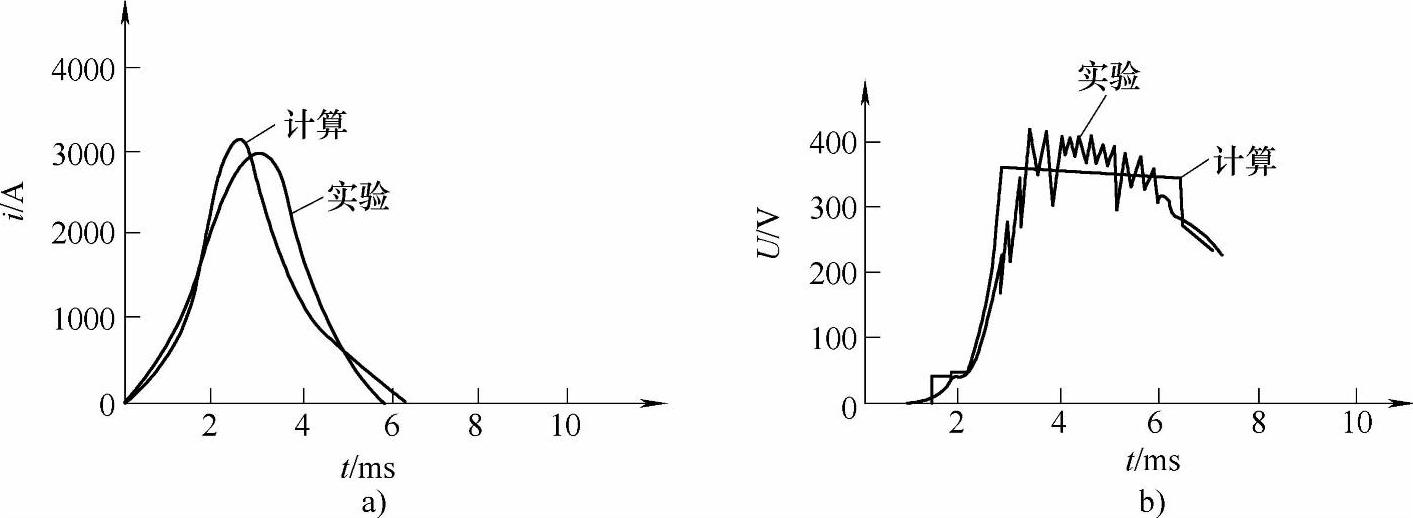
图8-7 计算与实测对比
a）电流波形 b）电压波形
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
开断试验方法及其限制与应用分析详细阅读
在积木式结构中，串联各单元的结构、工作条件、工作状态是基本相同的，只需取一个单元进行试验，因此实际试验电压就可以降低。这是一种受试验设备限制，不得已而采用的间接试验方法，以两次不同情况下的试验结果推断出的开断能力，等价性和可靠性均较差。目前分步试验已不能作为性能的验证试验，但可作为研究性试验，用以确定试品的最大开断电流。......
2023-07-02
-
电流开断后绝缘恢复特性分析详细阅读
此时，断路器触头间绝缘强度的恢复及其变化，是该断路器的固有特性，称为冷态绝缘恢复特性或空载绝缘恢复特性。断路器冷态恢复特性，由触头形状、分闸距离和灭弧介质的压力变化情况等决定。在各种断路器中提高弧隙介质强度的主要措施有：①采用介质强度高的灭弧介质；②采用各种结构的灭弧装置来加强电弧的冷却；③加速拉长电弧，提高介质强度恢复速度。......
2023-07-02
-
空载长线开断试验优化详细阅读
切空载长线的性能必须由制造单位提出保证。当A相发生短路后，B、C相首、末端的断路器动作不同期，后跳开的断路器是切空载长线；当A相故障仍然存在，三相断路器重合失败再次分断，B、C相上首末端的断路器仍然不同期，因而后开断的那一相断路器是重复的切断空载长线—此种情况下的操作方式为“分—0.3s—合分”。如果是以三相断路器进行三相试验，则不需要控制相位，只需要进行10次试验即可。......
2023-07-02
-
短路开断试验的规定和要求详细阅读
短路开断试验的目的是考核断路器在规定的恢复电压作用下，开断短路电流的能力。为使试验能够真实地反映断路器的实际运行情况，我国有关高压断路器的标准中，对短路开断试验的内容和方法都作了具体的规定。......
2023-07-02
-
失步开断、关合能力试验详解详细阅读
目前，IEC所规定的，也为各国所引用的联络用断路器在反相下的开断电流额定值为断路器额定短路开断电流值的25%。因此，在进行反相开断试验时均只考虑单相，但电流和电压按首开相考虑。在国际电工委员会和我国标准中确定失步开断的恢复电压时，考虑到衰减，对两端均接地或均不接地的系统而言分别取恢复电压为2Up或2.5Up。失步开断时恢复电压的振幅系数取为1.25，这是IEC的推荐确定的。失步开断电流值不大，因此，长短燃弧时间的差异并不显著。......
2023-07-02
-
开断能力试验等价性研究详细阅读
为了进行开断能力试验必须要有大容量的电源。为此，研究以较少的设备和投资去进行所需开断能力试验的方法得到很大的重视。试验断路器开断能力的方法很多，无论采用何种方法，均必须注意试验条件与被试断路器在实际系统中应用的等价性。特别是近年来高压断路器的电压等级和容量发展很快，对试验条件和设备的要求更高，试验方法和等价性更为重要。......
2023-07-02
-
近区故障开断试验解析与优化详细阅读
我国国家标准GB/T 4474—1992规定，额定电压63kV级及以上，额定短路开断电流大于12.5kA，现行IEC标准也规定，对额定电压为52kV及以上，额定短路开断电流超过12.5kA，且直接与架空线相联的三相断路器要求进行近区故障的开断试验。对近区故障而言，明显地存在长短燃弧时间的差异。......
2023-07-02
相关推荐