迈锡尼古城——神话之城位于希腊南岛伯罗奔尼斯东北部的古城迈锡尼，因为神话和宝藏的传说吸引着历代人们前往一探究竟。1874年，谢里曼开始开拓迈锡尼古城的遗址，结果两年后，他真的发掘了一个埋藏的旧世界，用荷马的史诗去诠释历史和那神秘的希腊。但迈锡尼古城废墟仍旧保持着那份神秘，充满了神话及神奇的魅力在向游客招手，也吸引着众多考古学者想要不断发现它的宝藏和秘密。......
2024-06-10
尼迈亚电弧的简单数学模型优化
【摘要】：简单的尼迈亚模型是一种经验公式类型的电弧数学模型，按图8-1所示，断路器开断过程可分成4个过程，它们是1）瞬动电磁铁动作过程；2）电弧停滞过程；3）电弧运动过程；4）电弧进入电弧栅片熄灭过程。经过停滞阶段后，电弧开始运动，迅速从动触头转移到导弧板，并在磁场力的作用下向栅片运动，计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型，这里介绍尼迈亚模型，它由L.Niemeyer博士于1984年提出[1]。
简单的尼迈亚（Niemeyer）模型是一种经验公式类型的电弧数学模型，按图8-1所示，断路器开断过程可分成4个过程，它们是1）瞬动电磁铁动作过程；2）电弧停滞过程；3）电弧运动过程；4）电弧进入电弧栅片熄灭过程。
在电弧停滞阶段，一定要当电弧拉长到极限长度xcrit，电弧才开始运动，根据J.G.J.Sloot等人的试验[4]，这一长度一般为xcrit=2mm。由于这时电弧虽已产生，但是不运动，因而出现了电弧电压Uarc，由于弧柱压降很小，因而可近似认为Uarc等于极间压降ΔU，一般ΔU=20～25V。
经过停滞阶段后，电弧开始运动，迅速从动触头转移到导弧板，并在磁场力的作用下向栅片运动，计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型，这里介绍尼迈亚模型，它由L.Niemeyer博士于1984年提出[1]。电弧运动所受电动力为
Fm=gli2 （8-2）
式中 g——比例常数；
l——电弧平均长度，对微型断路器来说，可取导弧片之间距离；
i——电弧电流。
另一方面电弧受到质量M惯性力的减速，假定这一惯性力与电弧开始运动瞬间的电流is有关，即
式中 v——电弧运动速度；
C——与结构有关的常数。
取Fm=FR可得
令
式中 xch——由触头到电弧栅片的距离；
将式（8-5）代入式（8-4），可得
求解（8-6）微分方程，可得电弧运动距离x与时间的关系，即x=f（t）。若认为电弧电压Uarc与电弧运动距离x成正比，则
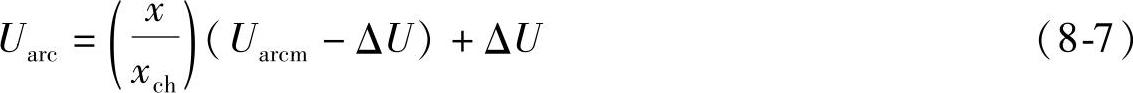
而Uarcm≈（n+1）ΔU （8-8）
式中 Uarcm——电弧电压峰值；
n——栅片数。
式（8-6）中常数βv系按样机开断试验的数据计算，对式（8-6）求积分得
上式中ts和is分别为电弧结束停滞阶段开始运动的时刻和该瞬间的电流，thd为电弧通过导弧板开始进入栅片的时刻。
电弧进入灭弧栅片后，依靠栅片把电弧分割成许多短弧而使电弧熄灭，这阶段电弧电压达最大值Uarcm，在这一电压作用下，电流被限制直至到零而熄弧。
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
喷口电弧的数学模型与描述技巧详细阅读
为了更好地分析电弧的加热作用，这里改变以往把电弧分成两段或三段考虑的传统观点，认为开断电弧对动触头内腔中的气体也有强烈的加热作用。断路器在开断电流过程中，电弧在强烈的气吹作用下，电弧根部弯曲于动触头内部。这里以位于动触头内部一微小段电弧长度lr1作为对Ⅲ部分中气体的热源，以喷口上游一微小段电弧lu作为Ⅱ部分中气体的热源，分别对电弧功率进行分析。......
2023-07-02
-
自力更生的艺术——莉迪亚·西格尔尼详细阅读
第22章自力更生的艺术在孩子年幼时，你可能通过让孩子养成某些习惯，来为他们将来的贫穷或富有、勤劳或懒惰、善良或邪恶打下基础。在那天到来之前，大部分公司取得成功的关键是自力更生。少雇员工的自力更生者知道情况可能会一团糟，但这可能会像我们在硅谷说的那样，是一个“高质量的问题”。......
2023-12-02
-
电弧二维动态数学模型探究详细阅读
对SF6断路器近区故障开断能力进行数值分析，首先应建立开断过程动态数学模型，因为电弧、灭弧室、喷口和动静触头等具有轴对称形状，且以灭弧室中轴线为其对称轴，所建数学模型在空间上为二维轴对称。采用K-ε两方程模型来描述湍流效应。......
2023-07-02
- 详细阅读
-
磁流体动力学电弧数学模型探讨详细阅读
磁流体动力学是研究导电流体在电磁场中运动规律的一门学科，其理论基础是流体力学和电磁学。基于对断路器电弧基本属性的研究，研究者逐步建立并不断完善电弧的磁流体动力学数学模型，使得数值仿真已经成为一种研究电弧的有效手段。由于在燃弧阶段，电弧等离子体处于LTE状态，考虑电弧产生的焦耳热和辐射的影响，用Navier-Stokes控制方程就可以建立断路器电弧的二维、三维磁流体动力学数学模型。......
2023-06-15
-
高效焊条电弧焊的方法优化详细阅读
在焊条电弧焊中，焊条的种类、规格等对焊接生产效率有着重大影响，高效率焊条包括两个方面：熔敷效率高和熔化速度快。通常用熔敷效率130%来区分一般铁粉焊条和高效铁粉焊条。......
2023-06-25
-
迈锡尼文明的消亡与希腊北方强盛的多利亚人有关详细阅读
迈锡尼文明消亡之谜观点之一：希腊北方的多利亚人强盛之后，南下攻城略地，逐步征服了除雅典以外的中希腊和伯罗奔尼撒各国，宣告了迈锡尼文明的灭亡。迈锡尼城是迈锡尼文明的中心，位于伯罗奔尼撒半岛东北部。海外贸易方面，迈锡尼虽然不像克里特岛的迈诺安文明那样倚重，但发达程度有过之无不及。入侵者在灭亡迈锡尼的物质文明后，并没有继承发扬它灿烂的精神成果。无论如何，迈锡尼文明迅速衰落是个不争的事实。......
2024-09-16
相关推荐