合闸相角对电动稳定性的影响分析

2025-09-29 百科知识版权反馈

【摘要】：GB14048.2仅对短时耐受实验中不同电流下的功率因数、冲击系数等进行了要求，并未对合闸相角进行规定。这主要是因为电流相间邻近效应主要体现在某相电流峰值时其他两相电流在该相导体内的感应电流方向，而合闸相角的改变不影响三相电流的相序，故其不影响某相电流峰值时其他两相电流在该相导体内的感应电流方向。

GB14048.2仅对短时耐受实验中不同电流下的功率因数、冲击系数等进行了要求，并未对合闸相角进行规定。改变合闸相角，可以在保证冲击系数的前提下，决定具体哪一相承受最大电流，由（7-1）可知，当合闸相角ψ分别为φ-π/2、φ+π/6、φ+5π/6时，A相、B相、C相分别约在9.6ms时，达到2.2倍短路电流周期分量有效值（55kA）。虽然，这三种情况下，短路电流最大值相等，但是邻近效应会影响各相总电流在各动导电杆上分布规律，继而影响短时耐受过程初始阶段的电动稳定性。为了突出邻近效应的作用，计算中忽略总电动斥力和温度对导电斑点半径的影响，本节研究内容中如无特殊说明，则短路电流为55kA。

如图7-31所示，合闸相角对短时耐受过程初始阶段动导电杆电流峰值分布的形态影响不大，A相电流峰值呈凹形分布，B相和C相电流峰值呈斜坡分布，相较而言，B相电流峰值分布更不均匀些。这主要是因为电流相间邻近效应主要体现在某相电流峰值时其他两相电流在该相导体内的感应电流方向，而合闸相角的改变不影响三相电流的相序，故其不影响某相电流峰值时其他两相电流在该相导体内的感应电流方向。但是合闸相角决定了哪一相耐受最大短路电流，由于B相电流分布最不均匀，这就造成ψ=φ+π/6时B₁动导电杆的电流峰值最大，约为2.5I_M，其中I_M=55kA/5，表示动导电杆平均短路电流周期分量有效值，即此时B₁瞬时电流峰值的冲击系数为2.5，该值大于总短路电流的冲击系数2.2。此外，ψ=φ-π/2时，A₁动导电杆瞬时电流峰值的冲击系数为2.3；ψ=φ+5π/6时，C₁动导电杆瞬时电流峰值的冲击系数为2.4。

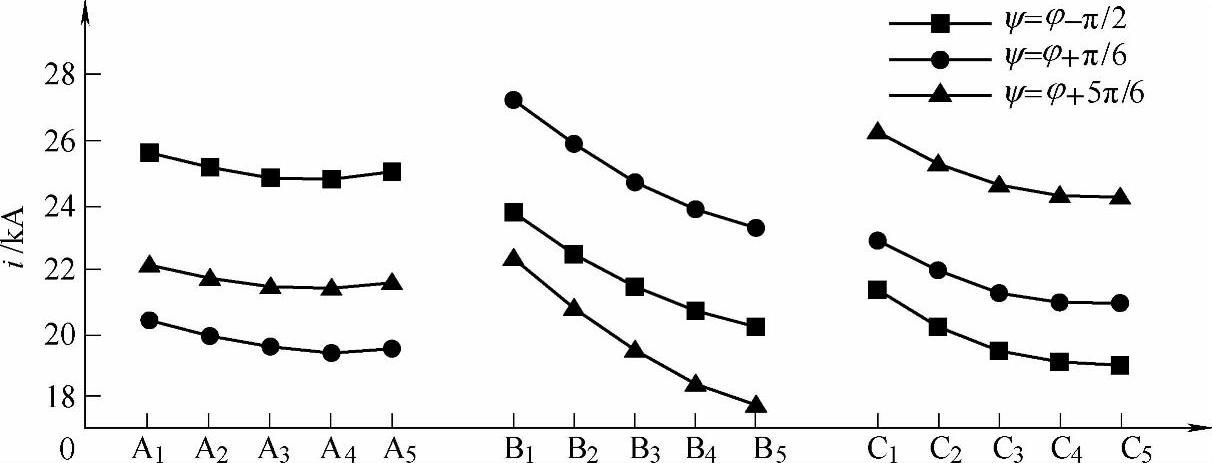
图7-31 合闸相角各动导电杆峰值电流的影响

由于电动斥力与电流平方的相关性，合闸相角对动导电杆上电动斥力峰值T_r的影响与其电流峰值分布影响类似，如图7-32所示，当合闸相角分别为φ-π/2、φ+π/6和φ+π/6时，动导电杆上最大电动斥力矩分别为2.23N·m（A₁）、2.60N·m（B₁）和2.38N·m（C₁）。

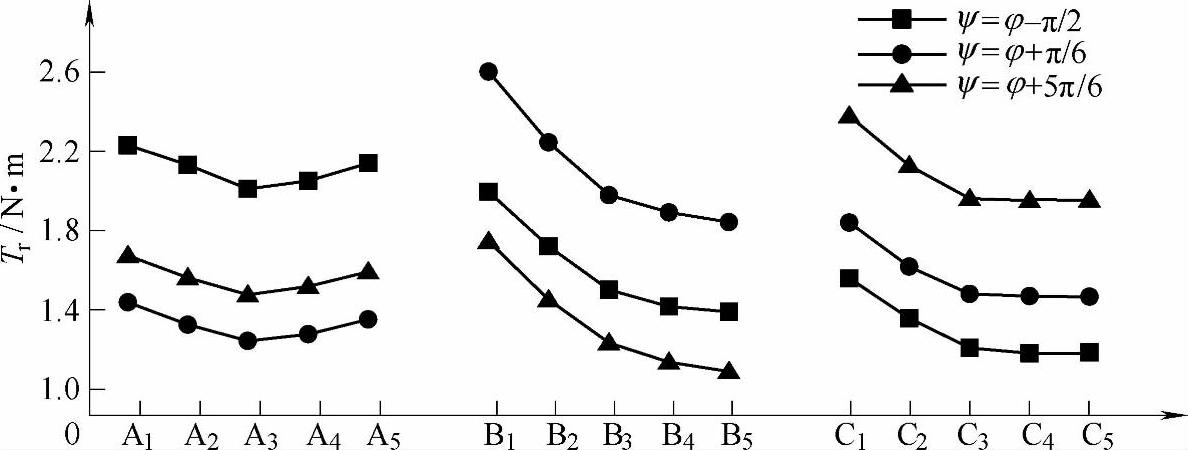
图7-32 合闸相角各动导电杆电动斥力峰值的影响

合闸相角对动导电杆侧偏力矩峰值和滑动力矩峰值的影响如图7-33和图7-34所示，同样地，合闸相角不影响其分布形态，只影响其具体数值大小。可以看出ψ=φ+π/6时，A₅动导电杆的拧转力矩最大；ψ=φ+π/6时，B₁动导电杆拧转力矩最大；ψ=φ+π/6时，C1动导电杆的拧转力矩最大。对比这三种合闸相角下的最大拧转力矩，其值相当，最大侧偏力矩约为3N·m，最大滑动力矩约为2N·m。(https://www.chuimin.cn)

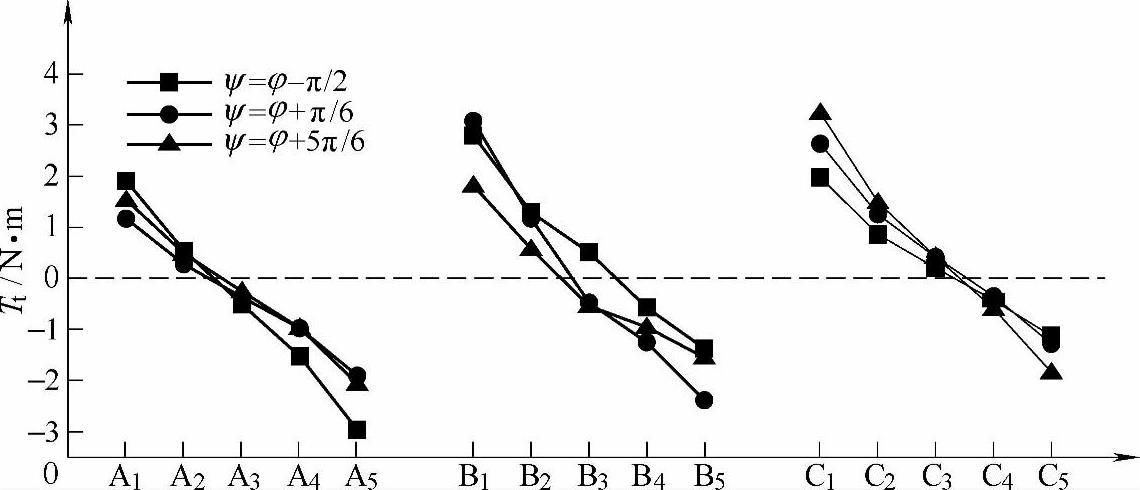
图7-33 合闸相角各动导电杆侧偏力矩峰值的影响

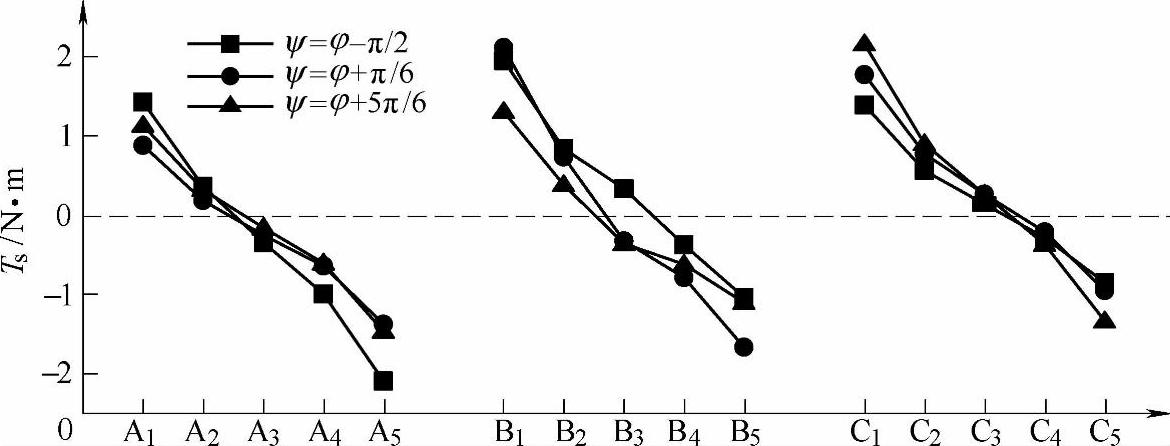
图7-34 合闸相角各动导电杆滑动力矩峰值的影响

目前，GB14048.2仅对短耐实验中不同电流下的功率因数、冲击系数等提出了要求，并未对合闸相角进行规定。

通过上述框架断路器三相触头系统电动稳定性模型研究发现：虽然合闸相角不影响三相多并联动导电杆电流的分布规律，但改变合闸相角，可以在保证冲击系数的前提下，决定具体哪一相承受最大电流，合闸相角为φ+π/6，即当B相承载最大电流时，B₁动导电杆上的电流峰值、电动斥力峰值和拧转力矩峰值最大，故其电动稳定性最差。根据系统稳定性短板效应，短时耐受实验时，选取合闸相角为φ+π/6时，使中间相承受最大电流的试验条件最为严酷。

合闸相角对电动稳定性的影响分析

相关推荐