热稳定性计算模型探究

2023-06-15 百科知识版权反馈

【摘要】：图7-21 热稳定性计算流程图最后，总载荷时间超过1s，计算结束，获得各个载荷步内电流有效值、导体温度、电动斥力矩、侧偏力矩和滑动力矩的分布规律。此外，为了考虑短时耐受过程初始阶段暂态电流对热稳定性的影响，依据三相暂态电流表达式，利用等效原则，将60ms时间内各个载荷步内短路电流换算为正弦电流进行加载。

一般认为，导电斑点温度会受到瞬态电流的波动影响。如果考虑导电斑点瞬态温度随短路电流变化的影响，进行长达1s时间的热稳定性仿真计算，一方面计算量太大，以50Hz正弦电流为例，若步长为0.5ms，计算1s时间内短时耐受过程需要2000个载荷步，大大延长了计算时间，另一方面基于动网格的电-磁-热瞬态非线性直接耦合模型收敛难度较大，因此，非常有必要从工程角度出发简化上述计算过程。采用图7-21所示的计算流程来研究框架断路器触头系统在短时耐受过程中的热稳定性，其主要思路是将上述物理量的瞬时相互作用过程，简化为载荷步内平均值的相互作用。

首先，初始化温度T，时间t和迭代步数n，并利用初始导电桥模型建立三相触头系统三维有限元谐波电磁耦合模型，考虑邻近效应和集肤效应，计算得到导体上平均发热功率分布和各个动导电杆归算到触头上电动力在载荷步内的平均值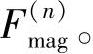

其次，通过三相触头系统三维有限元瞬态热传导模型，计算导体在该载荷步内瞬时温度分布和各个导电斑点表面温度在载荷步内的平均值T^（n）；一方面根据各个导电斑点表面温度平均值插值获得导电斑点布氏硬度，另一方面根据总电动斥力矩平均值和触头弹簧力获得接触压力；然后，利用Holm公式计算各导电桥在载荷步内的平均半径r_j^（n）。

若两次迭代结果各个导电桥半径相差都小于10^-5m，且各个导电斑点温度差都小于1℃，则认为该载荷步计算收敛，并进行下一载荷步的计算；否则更新导电桥半径和导体温度，进行迭代计算。

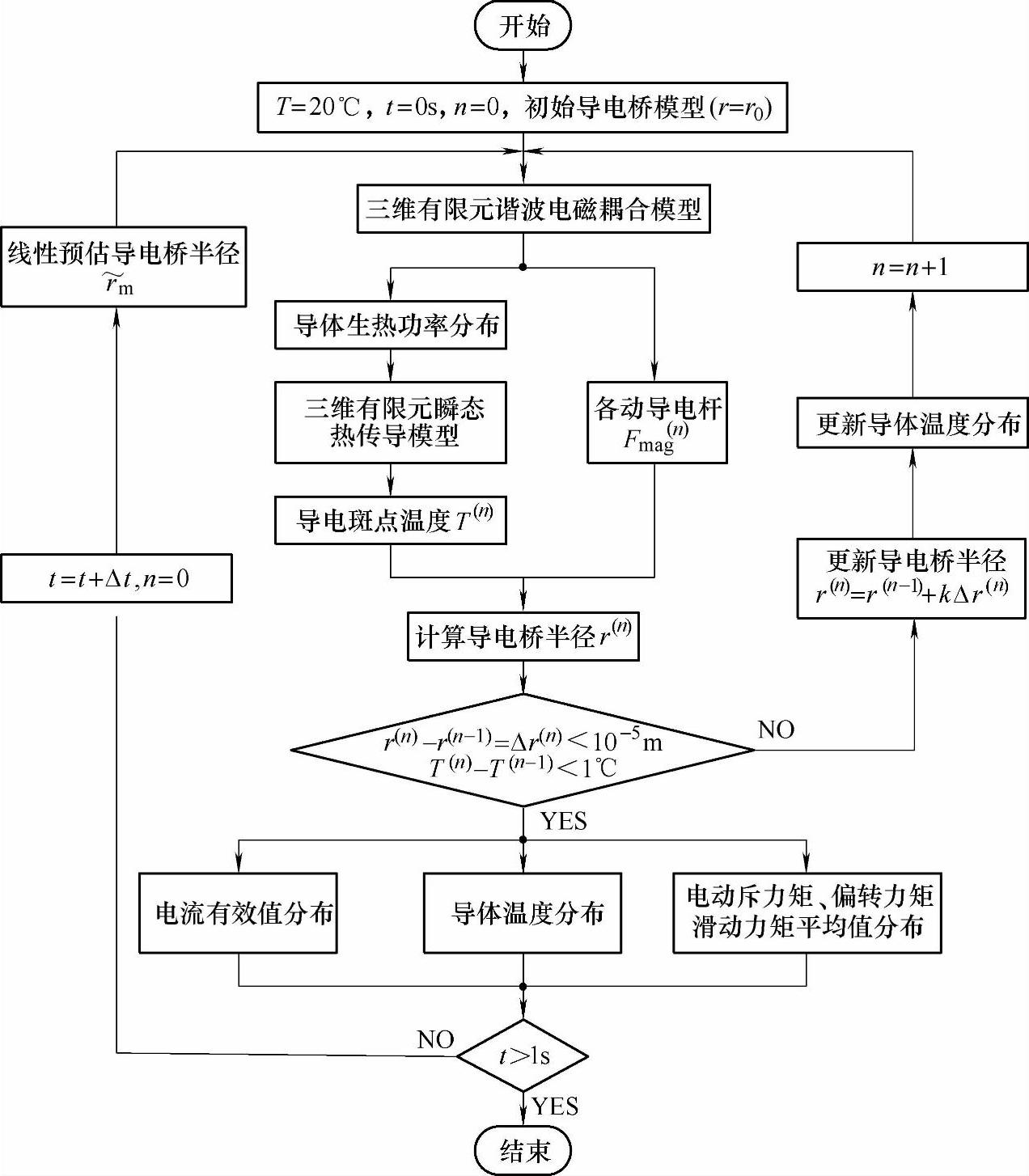
图7-21 热稳定性计算流程图

最后，总载荷时间超过1s，计算结束，获得各个载荷步内电流有效值、导体温度、电动斥力矩、侧偏力矩和滑动力矩的分布规律。

在迭代计算中发现导电桥半径对各物理量大小影响较大，是迭代收敛的关键，为了加快收敛速度，在各个载荷步计算开始前，利用前两个已收敛载荷步的导电桥半径，根据式（7-

3）线性预测该载荷步的导电桥半径：

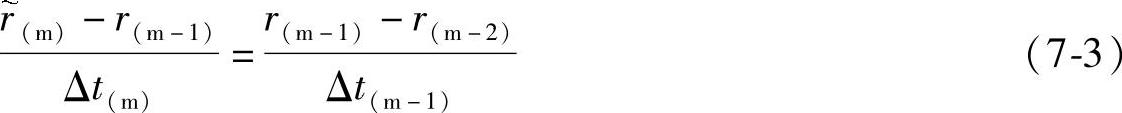
式中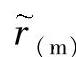——第m个载荷步导电桥半

径预测值；

r_（m-1），r_（m-2）——分别为第m-1和m-2载荷步导电桥半径收敛值；

Δt（m），Δt（m-1）——分别为第m个和第m-1个载荷步时间步长。

图7-22 导电斑点半径振荡收敛过程

此外，若某一载荷步内的迭代过程中导电桥半径出现如图7-22所示的振荡收敛过程，即Δr^（n-1）×Δr^（n）<0，在更新导电桥半径时，可为导电桥半径变化量添加松弛因子k=0.5，即r^（n）=r^（n-1）+0.5×Δr^（n），从而加快收敛速度，一般可在3个迭代步内收敛。

上述计算过程中的电阻率、热导率、热容都根据迭代过程中温度的变化而进行插值计算。而触头材料布氏硬度随温度的变化，直接影响着导电斑点的大小，可采用以下方法进行近似计算：

框架断路器一般采用非对称配对触头，动触头选用抗熔焊能力较强、耐烧蚀的触头材料，如AgW合金，其布氏硬度较高；静触头选用导热和导电能力较强的触头材料，如AgNi合金，其布氏硬度较低。导电斑点半径主要与布氏硬度较低的触头材料有关。

利用HB-3000B-I型布氏硬度计测得某牌号静触头常温下的硬度为375MPa。金属硬度随温度变化很大，因此静触头材料硬度的温度系数对计算结果的准确性非常重要，但是公开发表的文献中，关于AgNi触头材料在高温下硬度的报道较少。一般认为，大多金属（包括金属Ag和金属Ni）的硬度与温度的关系满足：

H=Aexp（-BT）（7-4）

式中 A——固有硬度（Intrinsic hardness），即T为0时的硬度（MPa）；

B——软化系数（Soften coefficient）（K^-1）；

上式系数A和B有两组值，在金属软化温度T_s前定义为A₁、B₁；在软化温度后定义为A₂、B₂，软化温度一般为金属熔点T_m的一半。金属Ag和金属Ni的软化系数见表7-3，可以看出二者软化系数相近，而且本文实验中的静触头为细晶银，其银含量>95%，金属维氏硬度与布氏硬度数值差距不大，故以金属Ag的维氏硬度软化系数近似静触头的布氏硬度软化系数。同时，细晶银熔点约为960℃，故本文取静触头软化温度为480℃，利用式（7-4）拟合得到的静触头近似布氏硬度如图7-23所示，计算公式如（7-5）所示。

图7-23 近似的静触头布氏硬度

H=375×exp（-9.76×10^-4×（T-20℃）），T∈（20℃-480℃）

H=239×exp（-37.6×10^-4×（T-480℃）），T∈（480℃-960℃）（7-5）

表7-3 金属Ag和金属Ni软化系数

上述计算过程利用谐波电磁场方法计算平均电动斥力和发热功率，即半波平均值，因此瞬态热场分析的最小载荷步为10ms，载荷步为10ms的整数倍。短时耐受过程初期导电斑点温度上升速度较快，故设置最小载荷步，随着时间的推移，导电斑点温度上升速度变慢，载荷步逐渐增大。此外，为了考虑短时耐受过程初始阶段暂态电流对热稳定性的影响，依据三相暂态电流表达式，利用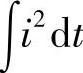等效原则，将60ms时间内各个载荷步内短路电流换算为正弦电流进行加载。

热稳定性计算模型探究

相关推荐