电路图一般由电路原理图、技术说明和标题栏组成。确切表明了各元器件间的组成、相互关系和工作原理。元器件明细栏均以表格的形式写在标题栏的上方。元器件明细栏（表）的组成明细栏一般由序号、代号、名称、数量、材料、质量、分区、备注等组成，也可按实际需要增加或减少。明细栏的尺寸与格式如图4-1所示。其顺序应是由上而下延伸，还可连续加页，但应在明细栏的下方配置标题栏，并在标题栏中填写与装配图相一致的名称和代号。......
2023-06-28
电动斥力分布的规律与应用
【摘要】：根据已有的研究成果，框架断路器动导电杆上70%的电动斥力来自于触头区域电流收缩引起的Holm力，其余来自导电回路。根据Holm力简化计算公式可知，Holm力与电流的平方成正比，故动导电杆上Tr峰值分布与电流峰值分布规律接近。图7-13 软连接截面磁感应强度的分布
动导电杆上的电动斥力Tr峰值分布如图7-12a所示，可以看出其分布规律与电流峰值分布规律接近：A相呈凹形分布，B相和C相呈斜坡分布。根据已有的研究成果，框架断路器动导电杆上70%的电动斥力来自于触头区域电流收缩引起的Holm力，其余来自导电回路。根据Holm力简化计算公式可知，Holm力与电流的平方成正比，故动导电杆上Tr峰值分布与电流峰值分布规律接近。
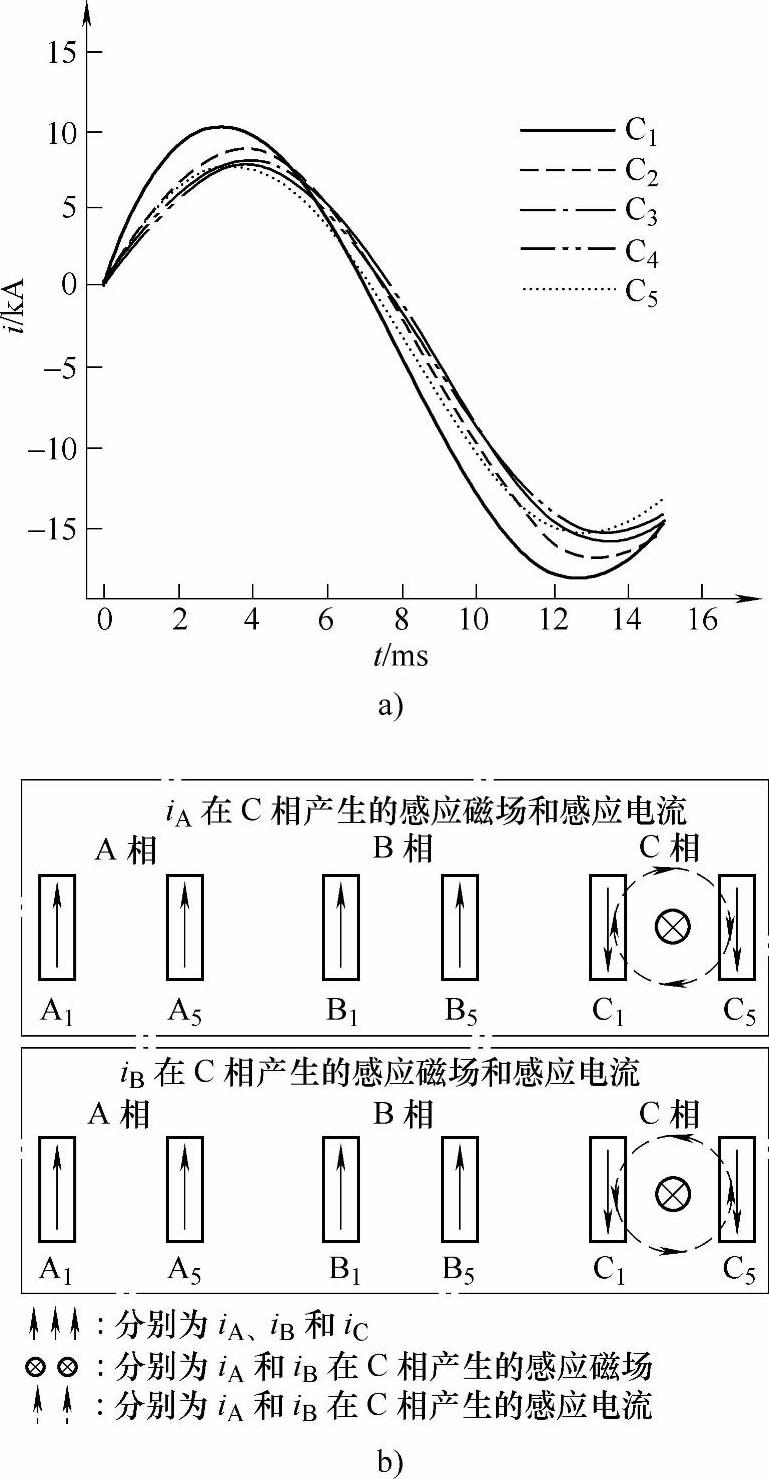
a）C相电流变化的曲线 b）感应电流示意图（t=6.5ms）
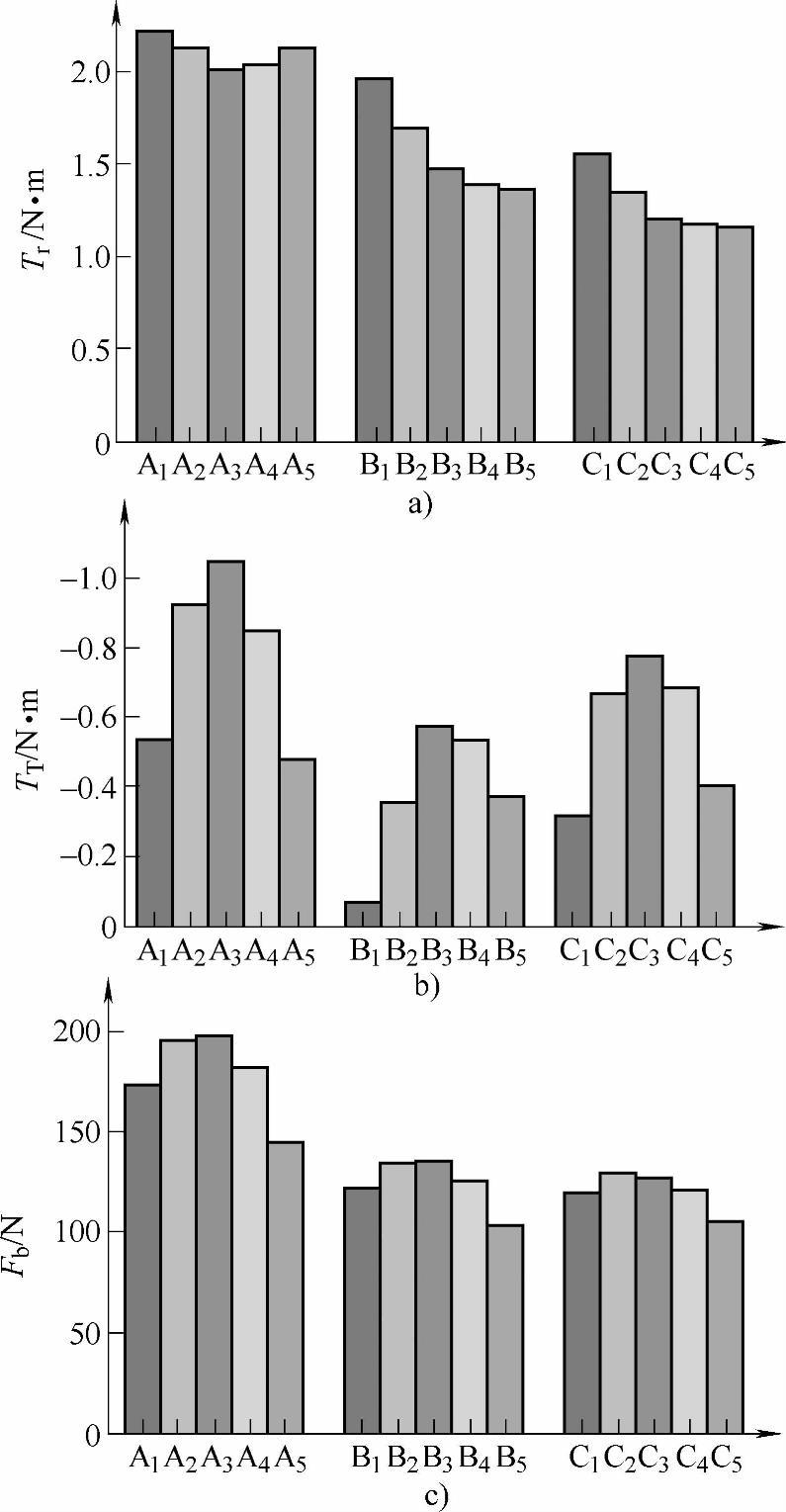
图7-12 电动斥力矩峰值的分布
a）动导电杆电动斥力矩Tr峰值的对比 b）总电动斥力矩TT c）软连接作用力Fb
考虑软连接作用力Fb后，总电动斥力矩TT的峰值分布如图7-12b所示，可以看出TT峰值为负值，即考虑软连接的作用后，TT不是斥开触头，而是压紧触头，这也是框架断路器设计中采用长度较长的软连接的一个重要因素；其次TT在各相动导电杆上都呈现凸形分布，这主要是因为TT=Tr-Fb×L，相比于Tr，Fb×L项占据主导，而各相动导电杆上的软连接补偿力Fb呈现凸形分布，如图7-12c所示。软连接补偿力Fb的分布规律可以根据软连接y-o-z截面上磁感应强度分布来解释，如图7-13所示，电流方向垂直纸面向里，可以看出相对于内侧动导电杆，外侧动导电杆Bz分量较小，这就造成靠外侧软连接上的洛伦兹力y分量FM-y=Ix×Bz较小，而Fb=FM-y/2。换言之：外侧软连接上Bz相对较小，造成了其FM-y相对较小，以致Fb在各相呈凸形分布，从而使得考虑软连接后，各相动导电杆上TT峰值也呈现凸形分布。
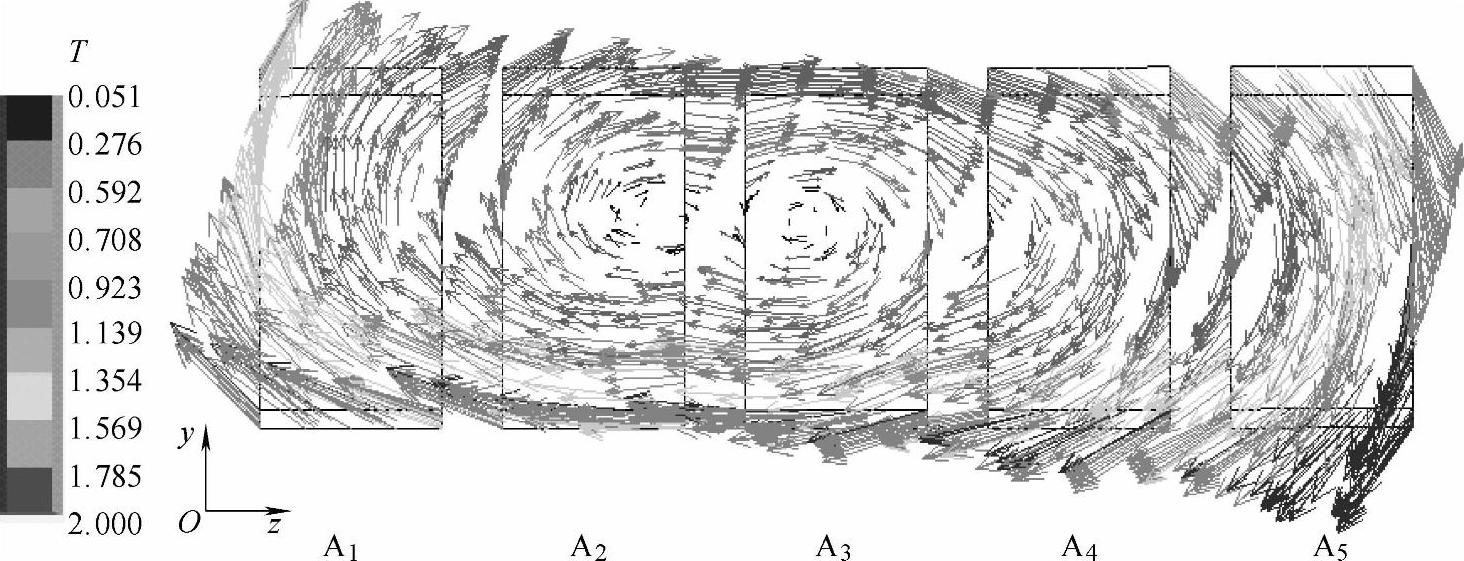
图7-13 软连接截面磁感应强度的分布（A相，10ms）
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
电动斥力对导电斑点面积的影响探究详细阅读
如图7-14所示，考虑了总电动斥力矩对导电斑点半径的影响后，各相中间动导电杆电流峰值增大，外侧动导电杆电流峰值减小，A相电流峰值呈不对称凸形分布，B相和C相电流峰值虽仍然呈现斜坡分布，但斜坡斜率变小。在电动斥力矩和软连接力的共同作用下，各动导电杆总电动斥力矩普遍增大，如图7-17所示。......
2023-06-15
-
动触头受电动斥力分析详细阅读
如上所述，在触头未斥开前，作用在动触头上的电动斥力包括触头间由于电流收缩产生霍姆力FH和导电回路产生的洛伦兹力FL。断路器导电回路上洛伦兹力FL一直存在至电弧熄灭，与电流的平方近似成正比关系。忽略涡流的影响，采用恒定场的方程来计算电流密度和磁通密度的分布，这样可以分三步来完成电动斥力的计算。图2-17 洛伦兹力计算流程图而对于低压断路器来说，动触头一般是在一个对转动轴的力矩M的作用下打开的，如图2-18所示。......
2023-06-15
-
纯弯曲横截面应力分布规律详细阅读
中性层与横截面的交线，称为中性轴。概括地说，纯弯曲时梁的所有横截面仍保持平面，并绕中性轴做相对转动，而纵向“纤维”则均处于单向受力状态。式（7-5）表明了梁横截面上正应力的变化规律。而要确定截面上某点的正应力的大小，还需建立应力与内力之间的静力关系。纯弯曲时梁横截面任意点的正应力计算公式，在一定条件下也适用于横力弯曲。......
2023-06-19
-
十二时辰经络养生：解析分布与流注规律详细阅读
《内经》有“夫十二经脉者，内属于脏腑，外络于肢节。”经脉在体表的分布规律：手三阴从胸走手，手三阳从手走头，足三阳从头走足，足三阴从足走胸腹。十二经脉在头面部的分布规律是：阳明在前（头面部），少阳在侧（头侧部），太阳在后（头后部）。......
2024-01-23
-
联肢剪力墙内力分布规律详细阅读
为了对联肢剪力墙的性能有深入的理解，首先介绍由连续化方法得到的联肢剪力墙的一些弹性内力计算公式，通过计算分析了解联肢剪力墙的主要规律。图7-12 倒三角分布荷载下k—α—ξ曲线族图7-13 连杆连接的独立墙肢整体系数α是联肢剪力墙的一个重要几何参数，整体系数α表示连梁与墙肢的相对刚度。整体系数α不仅与墙肢内力分布有关，它对连梁内力分布也有很大影响。......
2023-08-23
-
遗忘的含义、规律及应用详细阅读
遗忘是保持的对立面，保持的丧失就意味着遗忘的出现。他将实验结果绘制成一条曲线，这就是心理学上著名的艾宾浩斯遗忘曲线。该曲线反映了遗忘变量和时间变量的关系，揭示了遗忘的规律：遗忘的进程是不均衡的，遗忘的进程是先快后慢。图5-5艾宾浩斯遗忘曲线表5-2不同时间间隔的保持成绩艾宾浩斯遗忘曲线是通过无意义音节研究总结出来的，那么我们识记过的任何材料是不是两天以后都会忘记70%？......
2023-11-06
-
计及电动斥力效应的断路器分断过程仿真分析详细阅读
图2-24 分断过程的电动斥力的计算方法图2-25是分断过程作用在动触头上的电动斥力的仿真曲线。图2-25 电动斥力的仿真曲线图2-26是计及电动斥力作用下的触头主轴角位移的仿真结果与实验结果对比，造成仿真曲线与实验曲线在最后阶段有差异的原因是没有考虑电弧气动斥力。与手动脱扣比较，由于短路情况下电动斥力的作用，提高了动触头分断速度，机构的动作时间缩短了约1ms。......
2023-06-15
相关推荐