电动车稳定性计算模型

2023-06-15 百科知识版权反馈

【摘要】：图7-6 动导电杆电动斥力示意图图7-7 软连接受力示意图各动导电杆不仅可能会受到电动斥力的作用而发生斥开，还会在侧向电动力的作用下发生触头侧偏和触头滑移等破坏电接触稳定性的现象。由于短路电流暂态分量的缘故，三相断路器电流在20ms内相继达到各相最大值，因而短路电流作用的前20ms时间内是电动稳定性研究的重点。

随着触点温度的升高，导电斑点面积势必会由于触头材料硬度的减小而增大，这会造成动静触头间的Holm力减小。但是，为了简化计算以及获得较为严苛情况下的电动斥力，大多研究学者在单触头系统以及多并联触头系统电动斥力分析中，忽略温度的影响，因此本章在计算电动稳定性时也忽略导电斑点温度的影响。

图7-2描述了框架断路器多触头并联系统中，导电斑点半径与归算到触头上的总电动力（F_mag）的相互影响机制：①导电斑点半径r的增大，不但会减小触头间接触电阻R_e，还会减小动静触头间的Holm力（F_H）；②各动导电杆接触电阻的相对大小会影响其上电流i的分配；③电流的大小影响动静触头间的Holm力、动导电杆上的Lorentz力（F_L）和软连接上的受力（F_b），从而导致归算到触点的总电动力F_mag的变化；④最终，F_mag通过影响接触压力而改变导电斑点的半径。

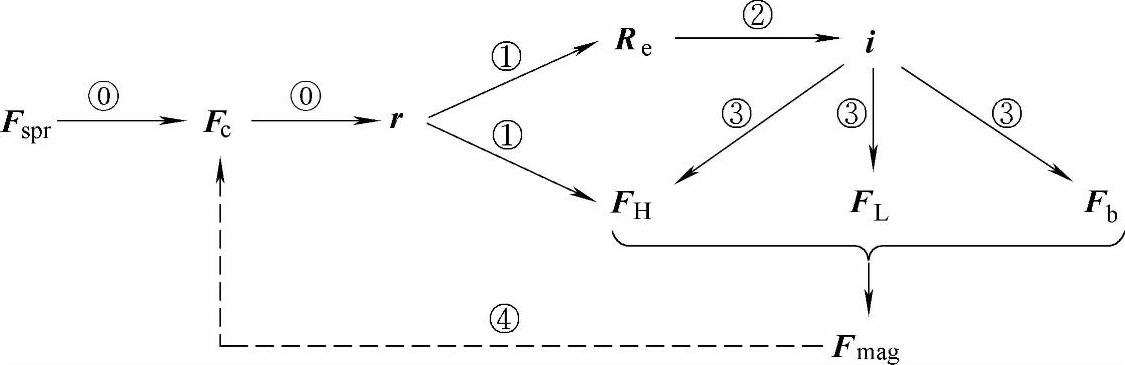
图7-2 导电桥半径与总电动斥力关系（忽略温度影响）

短时耐受过程中各相总电流i是时变的，上述物理量的相互作用过程是瞬时的，这就加剧了计算难度。如果将作用机制④直接纳入到模型中，一方面会增加计算量，延长研发周期；另一方面，目前商业计算软件结合动网格技术，进行电-磁瞬态非线性直接相互耦合模型和收敛难度较大，无疑增大了研发难度，因此非常有必要对作用机理④予以简化。本章采取的策略是在瞬态电磁耦合计算过程中，导电桥半径保持不变；当瞬态电磁耦合计算结束后，各导电桥半径利用各动导电杆总电动斥力的峰值来进行修正，然后重复上述瞬态电磁耦合计算过程，直至导电桥半径达到收敛准则。

具体计算流程如图7-3所示，首先，利用初始导电桥模型来建立三相触头系统三维有限元瞬态电磁耦合模型，进行15ms瞬态电磁耦合计算；其次，利用计算得到的各动导电杆总电动斥力F_mag峰值，根据公式（7-1）修正各导电桥半径，重新进行上述电磁耦合计算；若近两次迭代计算各个导电桥半径差都小于10^-5m，则认为迭代完成，整理实验结果，获得以各动导电杆电流峰值、总电动斥力矩峰值、侧偏力矩峰值和滑动力矩峰值为主的电动稳定性评价参数组的计算结果。

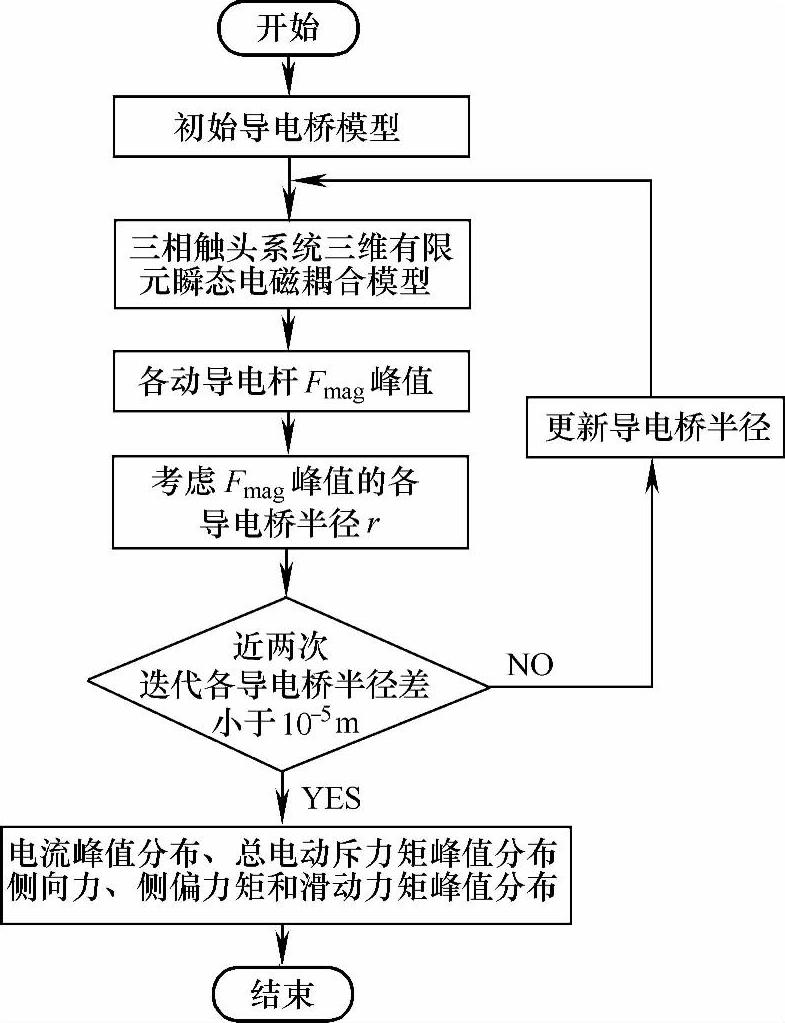
图7-3 电动稳定性计算流程图

式中 r——导电斑点半径（m）；

F_c——接触压力（N）；

ξ——经验系数，一般为0.3～0.6；

H——触头材料布氏硬度（MPa），H=375MPa。

上述计算流程在避免求解基于动网格的复杂电-磁瞬态非线性直接耦合模型的同时，可以保证各参数在电流峰值时刻的准确性，这主要是因为各相最大电磁力矩也发生在最大电流时刻附近，而电动稳定性分析主要关注的是电流和各电磁力矩的峰值。

以国产DW45系列额定电流为1600A三相框架断路器触头系统为分析对象，如图7-4所示，每相由5个平行并联的动导电杆、一个静触头、一个软连接、两个接线端子、一组灭弧栅片和若干导体组成。触头处于闭合状态，静触头固定不动，动触头可绕其转轴旋转，A相5个动导电杆依次命名为A₁、A₂、A₃、A₄和A₅，B相和C相动导电杆的命名规则一致。

框架断路器触头系统的短时耐受电流由外部电源提供，三相瞬态短路电流的表达式为

式中 I——短路电流周期分量有效值（A），其值为50kA；

t——时间（s）；

ψ——电压相角（rad）；

φ——功率因数角（rad）；

R——线路等效电阻（Ω）；

L——线路等效电感（H）；

f——频率（Hz），无特殊说明，f=50Hz。

根据国标GB14048.2规定，当短路电流I等于50kA时，线路的功率因素取0.25，即R/L=25.8π，此时若令ψ-φ=π/2，A相短路电流约在t=9.6ms时达到最大值103kA，约为周期分量有效值的2.1倍，B相和C相短路电流分别约在t=6.4ms和t=13.2ms时，分别达到峰值为-91.5kA和-82.8kA，如图7-5所示。

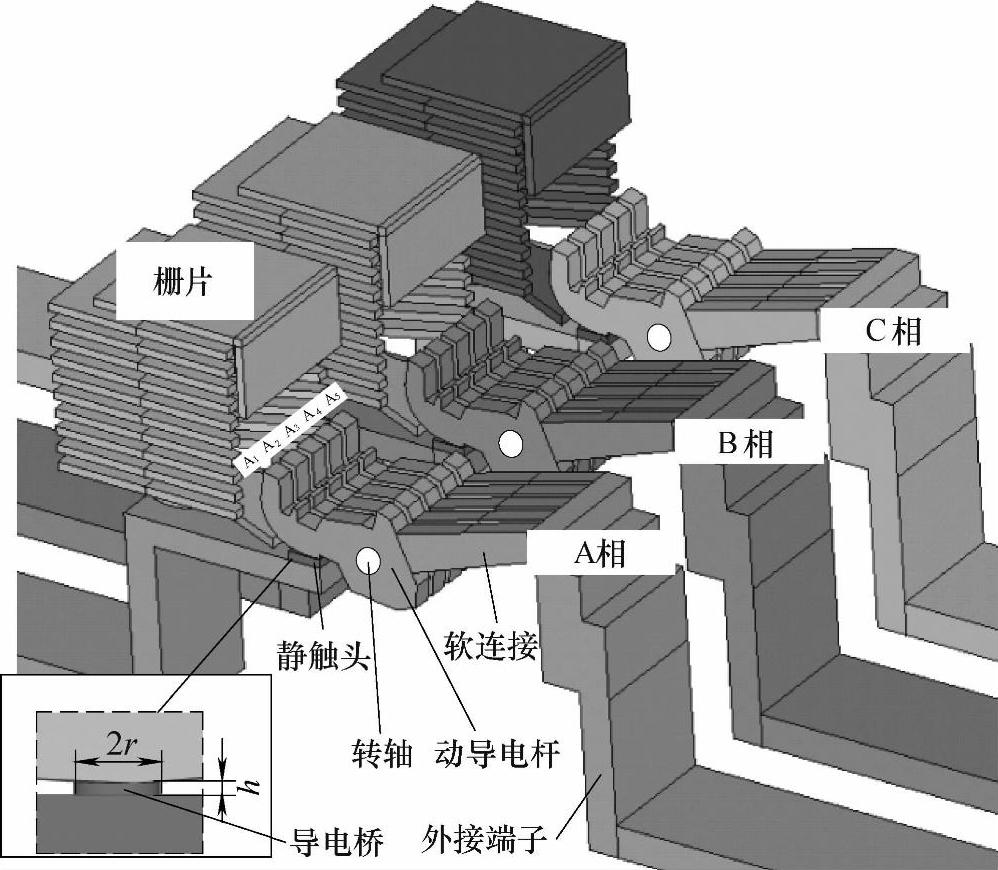
图7-4 框架断路器的触头及灭弧系统

触头系统的电动斥力不但决定了触头是否会斥开，还影响着触头部件承受的机械应力，因而正确计算框架断路器的电动斥力至关重要。动导电杆上的电动斥力F_r主要包括回路产生的洛伦兹（Lorentz）力F_L和动静触头接触点上电流收缩产生的霍姆（Holm）力F_H；此外，软连接受到电磁力的作用后，会对动导电杆产生提拉作用力F_B，如图7-6所示。因而，总电动斥力矩T_T=T_r-T_B=T_L+T_H-T_B，其中T_r、T_L、T_H、T_B分别为F_r、F_L、F_H、F_B的以触头转轴为中心归算的力矩形式。

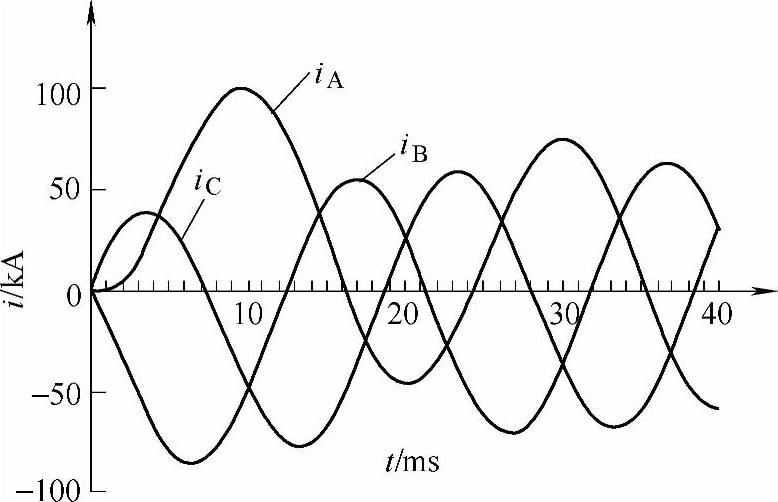
图7-5 三相短路电流波形

利用第6章介绍的导电桥模型法，在各动静触头间建立导电桥模型，来描述动静触头间电流线收缩现象，此时模型中动导电杆上洛伦兹力包含了回路产生的洛伦兹力F_L和动静触头接触点由于电流收缩产生的霍姆（Holm）力F_H。

软连接受力示意图如图7-7所示，主要包含两类型的外力：洛伦兹力F_M和两端焊点A和B沿软连接切线方向的作用力（F_A，F_B），将上述力按照局部坐标系分解，假设F_A-y=F_B-y，根据软连接外力平衡，则F_A-y=-F_M-y/2；基于作用力与反作用力大小相等，软连接对动导电杆作用力F_B=-F_A-y=F_M-y/2。

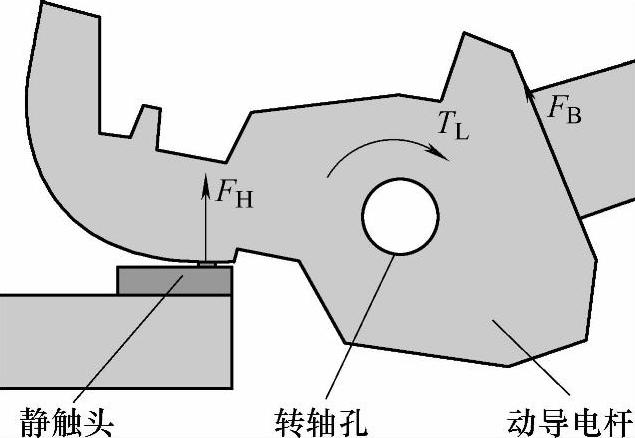
图7-6 动导电杆电动斥力示意图

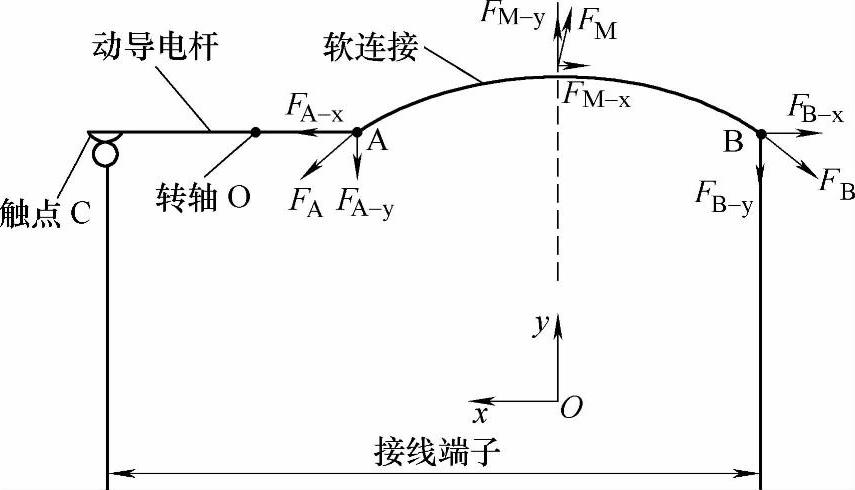
图7-7 软连接受力示意图

各动导电杆不仅可能会受到电动斥力的作用而发生斥开，还会在侧向电动力的作用下发生触头侧偏和触头滑移等破坏电接触稳定性的现象。触头发生侧偏和滑移现象的原因是动导电杆上存在着侧偏力矩T_t和滑动力矩T_s，其产生的原因和大小分布规律将在后文中将详细阐述。

在具体电磁计算中，在各个动导电杆上建立如图7-8的局部坐标系，局部坐标系原点位于转轴孔中心O；x轴为向量，其中C为动静触头触点；y轴垂直并指向上部；z轴垂直x-o-y平面指向纸面里，令F_B关于动导电杆转轴的力臂为L，则动导电杆上的总的电动斥力T_T=T_r-T_B=T_z-F_M-y/2×L，T_t=T_x，T_s=-T_y其中T_x、T_y和T_z分别为动导电杆上的分布电磁力在各个动导电杆局部坐标系的积分。

由于短路电流暂态分量的缘故，三相断路器电流在20ms内相继达到各相最大值，因而短路电流作用的前20ms时间内是电动稳定性研究的重点。利用三维有限元瞬态电磁计算方法，求解20ms内上述框架断路器三相触头系统的电动稳定性。

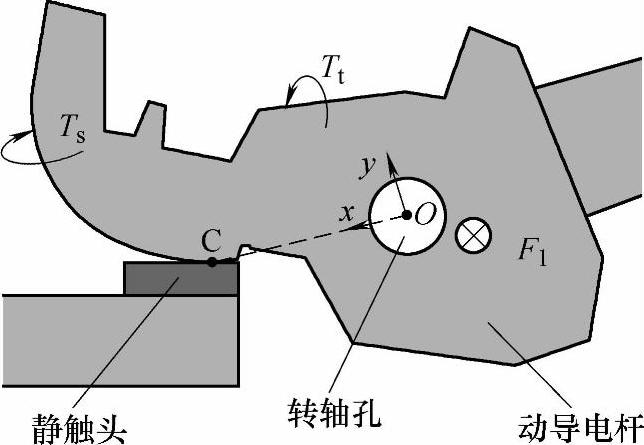
图7-8 动导电杆侧偏力矩和滑动力矩示意图

电动车稳定性计算模型

相关推荐