实验模型及方法详解

2025-09-29 百科知识版权反馈

【摘要】：实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的

实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。其中虚线部分所示为灭弧室，每一个灭弧室的尺寸均为36×32×20，静导电杆的厚度为2.5，动、静导电杆的宽度均为5，动、静触头的大小分别为7×4×2和7×7×2。出气口的大小为3×3和6×6两种。

灭弧室采用不饱和聚酯模塑料（DMC）材料，动、静导电杆和动、静触头分别为铜和银氧化锡（Ag/SnO₂），产气材料为POM。

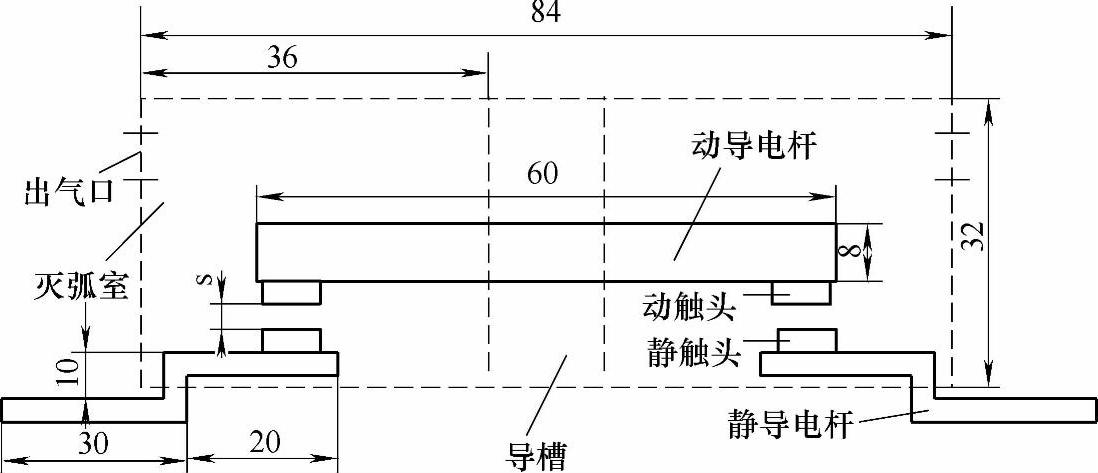
图6-25 气动斥力实验模型的平面图

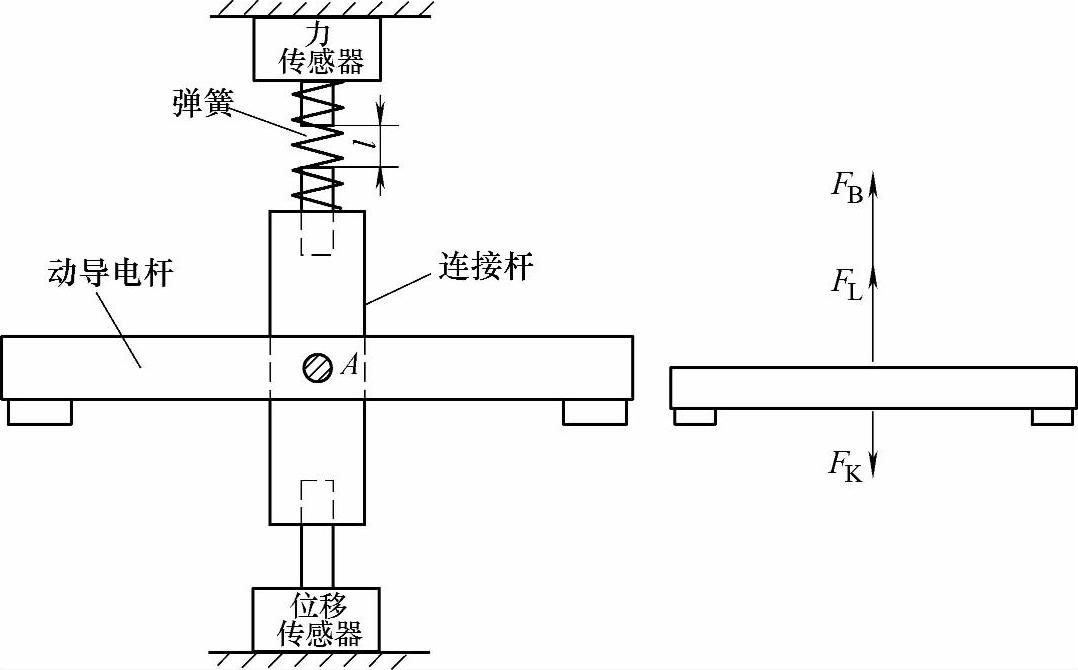
图6-26 气动斥力测试方法的原理图

测量方法的原理如图6-26所示。动导电杆通过螺钉固定在连接杆上的A点，实验时模型水平放置，初始时在一定的弹簧压力作用下，动静触头闭合，当短路电流到来后，在电动斥力F_L和气动斥力F_B的作用下，动触头开始运动，并带动连接杆在图6-25所示的导槽中滑动，连接杆的一端和电阻式位移传感器的测量杆相固定，以测量动导电杆的运动位移s随时间的变化过程，另一端通过弹簧和石英拉压传感器相连接，可测量弹簧作用在其上的力F_K，两个连接端有一段距离l，这也是留给动导电杆的最大位移量。

这样，作用在动导电杆上力就包括F_L、F_B和弹簧力F_K，且满足式（6-16）所示的关系式，其中m为连接杆、动导电杆等可动部分的质量。根据实验中测量到的s和F_K，求解该方程，就可以得到F_L和F_B的合力值，也即F。此外，由于F_K仅与弹簧的刚度系数和长度的变化量有关，因此力传感器并不是必须的。

图6-27为采用上述方法得到的一组电弧电流、电压和动导电杆位移的实验结果，弹簧的预压力为3N，电流峰值I_m为5.3kA，电压峰值为76V，最大位移为2.1mm。但是，由于位移传感器的测试精度以及模型中机械摩擦等因素的影响，位移的测量结果明显滞后于电流和电压。除了以上原因之外，电弧的热惯性也可能造成该现象。

为了克服这种问题，实验也可以在固定的动静触头间距条件下，采用熔丝引弧的方法，通过直接测量燃弧期间作用在动导电杆上的F_L和F_B的合力来完成。此时，只要将连接杆的一端固定在力传感器的测量引出端即可。下面的实验均是采用该方法进行的。

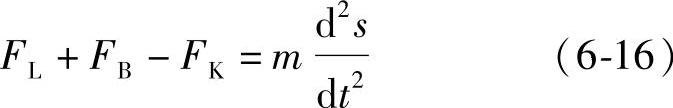
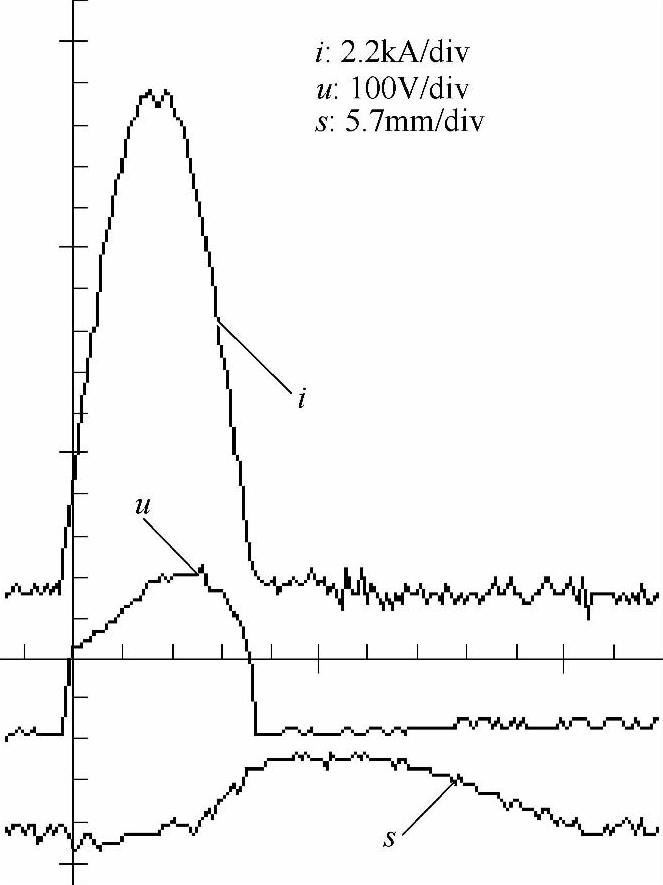
图6-27 I_m=5.3kA时的一组实验结果

实验同样采用频率为50Hz的大容量振荡回路提供短路电流，由于实验模型不具备开断较大短路电流的能力，在实验电路中串接一个低压塑壳断路器来开断电路，保证燃弧持续时间只有一个半波，以减小短路电流对于模型和触头系统的破坏。

在实验中，除了利用石英拉压传感器测量作用在动导电杆上的力F外，还通过分流器得到电弧电流，以及用高压探头测量电弧电压，最后用一台数字式存储示波器记录这些实验波形。

实验条件有以下三种：

1）在不同的预期短路电流（有效值为3～6kA），当出气口3×3时，针对5个不同的动、静触头间距s（=2、3、4、5、6mm）进行实验。

2）当s=2mm，出气口为3×3时，在灭弧室中两个触头区域均加入19mm×12mm的POM产气材料进行实验。(https://www.chuimin.cn)

3）当s=2mm时，没有产气材料，仅改变出气口大小为6×6。

根据以上的分析，由于实验中测得的力F为作用在动导电杆上的电动斥力F_L和气动斥力F_B的合力，为了得到气动斥力随时间的变化过程，就需要从合力中减掉电动斥力。

从6.3节可以看出，采用有限元方法可以对电动斥力进行较为准确的计算。为了便于分析，对电弧进行简化处理，认为电弧是连接动静触头的一段导体，然后利用ANSYS有限元分析软件，对图6-25所示的实验模型中的电动斥力进行了计算。

图6-28所示为当动、静触头的间距s=5mm，电流为4kA时1/4模型的电流密度分布。

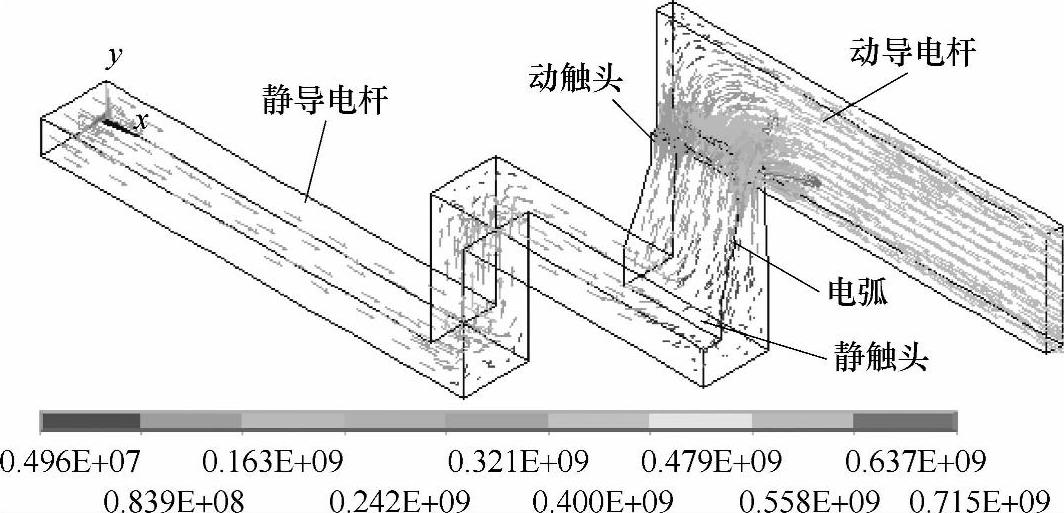
图6-28 导电回路的电流密度分布

表6-6为电流等于4kA、不同触头间距s时的电动斥力的计算结果。由于模型中不存在非线性铁磁物质，这样同一间距时电动斥力和电流的平方成正比例关系。计算结果也说明了这一关系，s=2mm，电流为6kA时，电动斥力的计算结果为9.32N，与4kA时相比，电流的平方比值为6²/4²=2.25，而力的比值为9.32/4.14=2.251。因此，根据表6-6的数据以及电动斥力与电流之间的关系，就可得到这些间距时任意电流作用下的电动斥力数值，从而求得作用在动导电杆上的气动斥力数值。

表6-6 电流为4kA时的电动斥力的计算结果

图6-29a所示为触头间距s=2mm，预期短路电流有效值为5kA，实际短路电流峰值I_m=4.2kA时的实验结果，其中F、u和i分别为作用在动导电杆上的力、电弧电压和电流；图6-29b为F达到峰值之前，F、气动斥力F_B、电动斥力F_L随时间的变化曲线。其中F_L曲线是基于表6-6的关于电动斥力的计算结果，根据电动斥力与电流的平方成正比例关系得到的。F_B曲线是测量得到的合力F和F_L的差值。应该指出的是，由于电弧电压的作用，使得实际的短路电流总是小于其预期值。

从图中可以看出，由于在实验电路中串接了一个用于开断电路的塑壳断路器，电弧电流只有一个半波。在起弧的时候，电弧电压有一个初始值U₀，随着电流的上升，电弧电压的数值也有一定的提高。在本实验条件下，U₀的变化范围为30～50V。

而测得的作用在动导电杆上的力同样在起弧时有一个初始值，开始时随着电流的上升而增大，但是很快达到峰值（在本实验的所有结果中，力峰值均在电流峰值之前）。此后，随着作用在动导电杆上斥力的减小，连接杆和保持固定触头间距部分的变形，以及传感器应变片开始恢复反弹，使得作用在传感器上的力有一个反方向的冲击。

本实验目的是分析气动斥力的作用特性，以及各种因素对气动斥力的影响规律。这样，根据实验结果，以下仅对作用在动导电杆上的力达到峰值之前的过程进行分析，并由此对峰值以后的气动斥力作用进行推算。应该指出的是，以上的实验方法分析也提到，测量动导电杆的位移可从动态的角度来分析气动斥力。

此外，需要说明的是，为了更好地对实验结果进行分析，认识气动斥力的特性，以下所有的F_B/（ui）随时间的变化曲线都是对根据实验得到的数据曲线采用FFT方法进行平滑处理的结果。

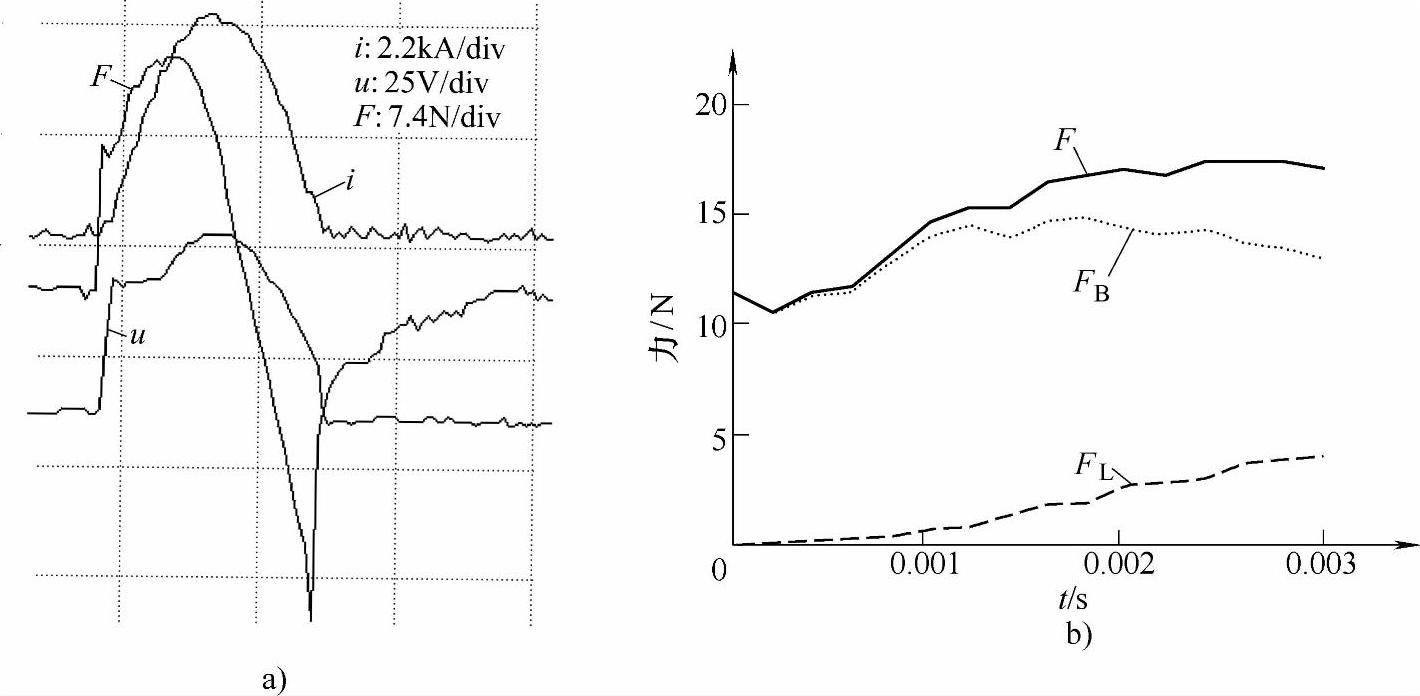
图6-29 s=2mm，I_m=4.2kA时的实验波形及电动斥力、气动斥力随时间的变化曲线

a）力、电弧电流和电压的实验波形图 b）合力、电动斥力、气动斥力随时间的变化曲线

实验模型及方法详解

相关推荐