如何确定塑壳断路器触头斥开时间和触头压力？

2023-06-15 百科知识版权反馈

【摘要】：图6-22 触头斥开时间计算流程图图6-22为计算触头斥开时间的迭代流程图。以6.4.1节中的CB2断路器产品为研究对象，在预期短路电流有效值为10kA条件下进行开断实验。这是因为CB2的触头预压力为4.4N，而当电流为2800A和2900A时，电动斥力分别等于4.3N和4.7N。一般来说，断路器瞬时脱扣器的动作电流为额定电流的12倍。对CB2来说，预压力的设计值可以通过下式得到：2×4.4/28252=1.59N。

基于6.2节中所示的电流-磁场-电动斥力之间的关系，采用三维有限元分析，可以得到作用在动导电杆上和触头上的电动斥力。由于该力和短路电流之间存在单调增的关系，不考虑铁磁物质的影响时，电动斥力与短路电流的平方成正比。而且在特定的短路条件下，短路电流和时间有一定的函数关系。这样就可以通过对上述过程的迭代处理，当电动斥力F等于触头预压力F_K时，迭代结束，此时对应的时间即为触头斥开的时间。

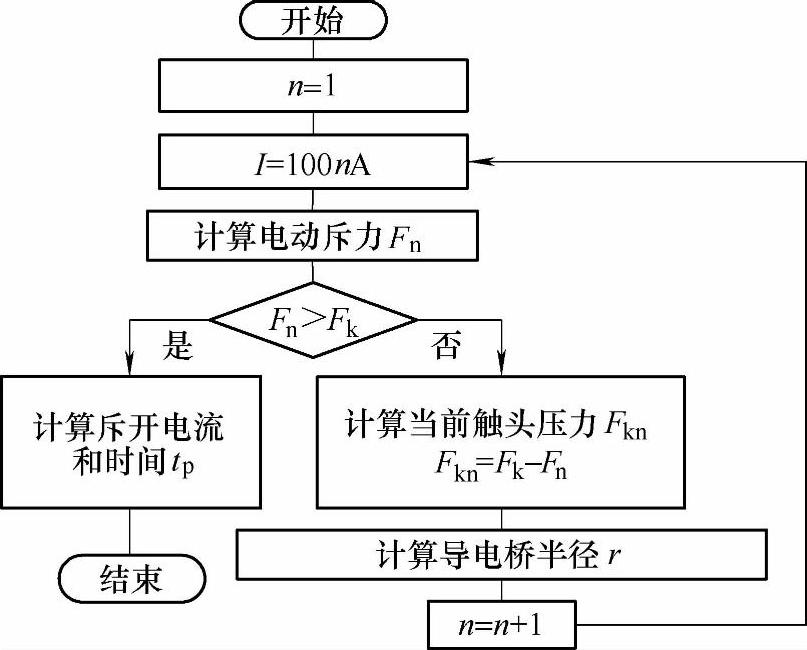
图6-22 触头斥开时间计算流程图

图6-22为计算触头斥开时间的迭代流程图。为了考虑电流对触头压力和相应的导电桥半径的影响，电动斥力、触头压力和导电桥半径每隔100A计算一次。

以6.4.1节中的CB2断路器产品为研究对象，在预期短路电流有效值为10kA条件下进行开断实验。图6-23为测量到的电弧电流和电弧电压波形。可以明显地看出，当分流器的电压上升到273mV时，也就是短路电流达到273mV/90μΩ=3033A时，时间为759μs时，动静触头之间的电压有一个突跳，这说明触头此刻在电动斥力的作用下打开，电弧产生，突跳电压值也就是阳极和阴极的电弧电压降。此时前，电流为正弦波，而且由于触头间接触电阻的存在，电压随着电流上升有一个很小的数值。此时后，由于电弧电压的存在及其限流作用，电流波形不再是正弦波。最后，当电流过零后，电弧熄灭。

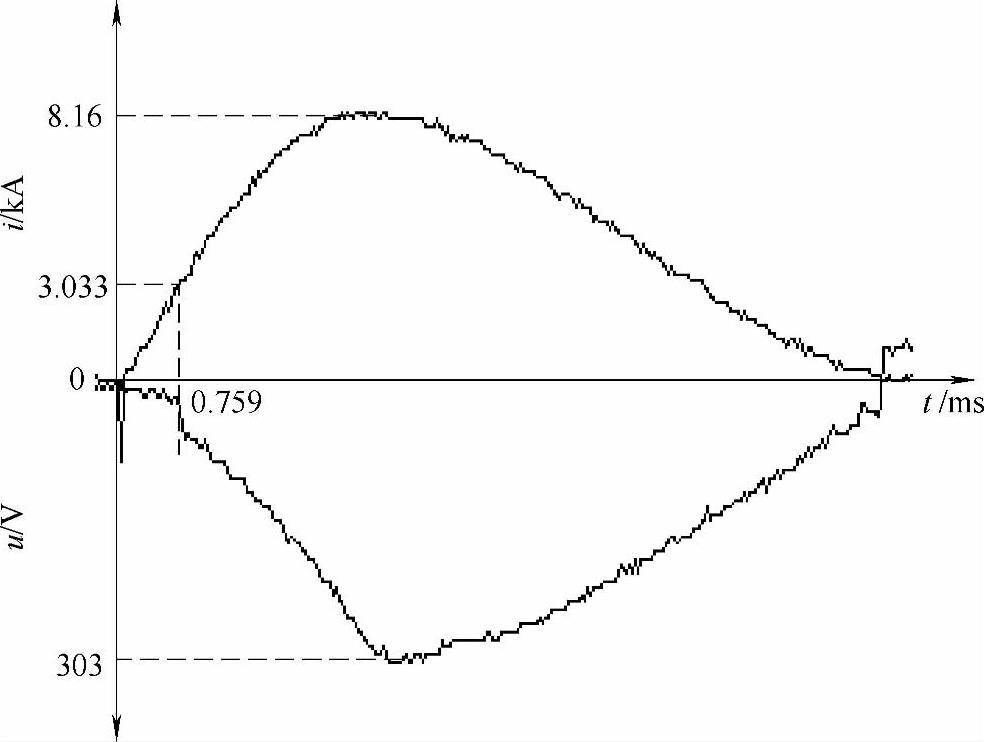
图6-23 CB2开断过程的电弧电流和电弧电压波形

对应于图6-22所示的迭代计算流程图，当电流达到2900A时迭代结束。这是因为CB2的触头预压力为4.4N，而当电流为2800A和2900A时，电动斥力分别等于4.3N和4.7N。图6-24为导电斑点半径随电流的变化关系。这样，就可以得到：当电流为2825A，时间为640μs时，触头开始斥开。而实验值为电流为3033A，时间为759μs时，触头斥开。考虑到动触头和主轴之间的摩擦等影响，计算值比实验值略小。

另一方面，忽略电流和电动斥力对导电斑点半径的影响，并认为触头压力保持在4.4N，计算结果电流为3020A，时间为674μs时，触头斥开。这样的计算结果和考虑导电斑点半径随电流变化时的结果较为近似。

因此，对特定的短路条件，可以用上述方法方便地计算出触头的斥开时间，以分析断路器的性能。

此外，如果忽略触头压力和导电斑点半径之间的关系，并假定电动斥力和电流的平方成一比例关系，就可以初步设计出比较理想的触头预压力。一般来说，断路器瞬时脱扣器的动作电流为额定电流的12倍。对CB2来说，预压力的设计值可以通过下式得到：（12×2^0.5×100）2×4.4/2825²=1.59N。在此基础上，考虑到脱扣器的安全裕量以及热动稳定性，就可以设计出一个比较优化的触头预压力数值。

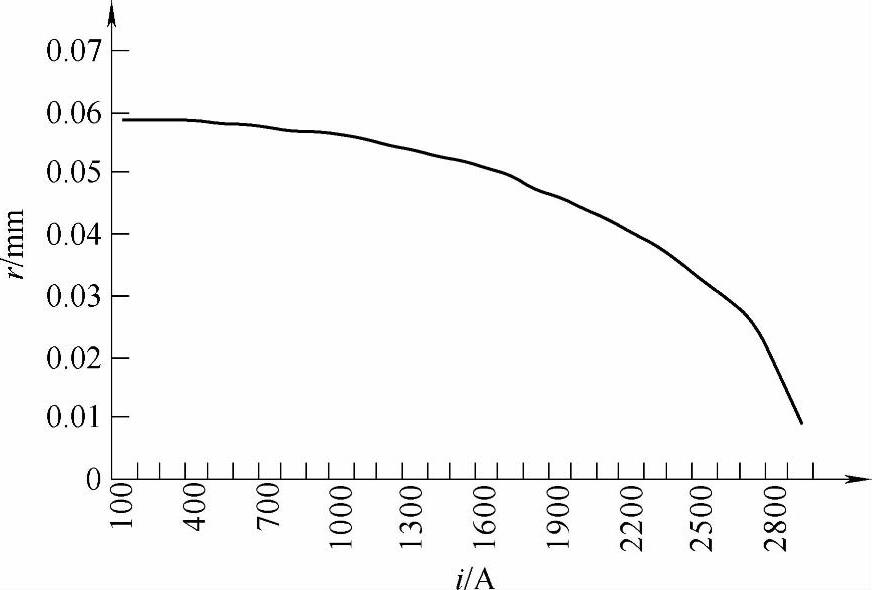
图6-24 导电斑点半径随电流的变化

如何确定塑壳断路器触头斥开时间和触头压力？

相关推荐