然而,随着颗粒体积分数的增大,炸药的脆性增加,更容易发生拉伸破坏。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。图8-35三种不同颗粒体积分数和颗粒分布细观结构模型的应力-应变曲线图8-36~图8-38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。从三种模型的计算结果可以发现,动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。......
2023-06-27
图6-19a,图6-19b,图6-19c分别为当电流为10kA时,CB1和CB3动、静导电杆,CB1动导电杆和动触头上的电流密度分布图。
对应于图6-18a右下角的电流方向和图6-19b不同,从图6-19a所示的CB1俯视图可以清晰地看到由于其静导电回路的U型弯曲导致图中1所示部分的电流方向和动导电杆相反。另外,本章所有分析都是相对于图6-19a所示的坐标系进行的,其中X、Y及Z轴正方向符合右手法则,在该图中,Y轴正方向垂直纸面向外。从6-19c可以看出,触头上由于电流收缩,其电流密度最大值比动导杆上高5个数量级。
图6-20a,图6-20b分别为沿CB1和CB3动导电杆上z方向的平均磁感应强度Bz和y方向上的平均力密度fy分布,其原点为动导电杆的左端,也就是图2-18中的A点。可以发现,靠近触头的区域,磁场和力密度均比较大,而且该区域远离转轴,力臂较大,因而可以认为,回路电动斥力,也就是Lorentz力FL主要取决于这部分。同时明显地看到CB1的磁场和力密度较CB3大。
在统一计算Holm力FH和Lorentz力FL的数值分析过程中,也可以认为作用在动导电杆上B点(见图2-18)的等效合力由两部分组成,即认为作用在动导电杆上的力为FL,作用在动触头上的力为FH。这一点可以通过下面的仿真来验证。对CB2,10kA电流时,不考虑触头间的电流收缩时,作用在动导电杆和动触头上的合力为15.66N;另一方面考虑触头间的电流收缩时,作用在动导电杆上力为12.34N,而作用在动触头上的力为30.98N。因此,为了便于接下来的分析,分别用FL和FH来近似描述作用在动导电杆和动触头上的电动斥力。
从表6-3中的对CB1的计算数据来看,电动斥力和电流的平方近似成正比例关系。表6-4所示为10kA电流时,5种模型的电动斥力计算结果。从两个表中可以看出,FH占整个电动斥力的70%左右。比较CB3和CB1的计算结果,将静导电杆的形状从水平U型改为平板型,电动斥力有所减小,说明水平U型通过改变电流的方向,有利于加强触头区域的磁场及相应的电动斥力,这一点也和图6-20的结果相一致。对CB5来说,由于没有栅片,和CB1相比,FL的数值减小了40%左右,说明铁磁物质可以有效地加强动导电杆上的磁场。对CB4来说,通过改变CB2的栅片尺寸并加入U型电机槽后,电动斥力也有所增大。同时,这种改进也有利于将产气材料固定在电机槽内侧,利用新的气吹灭弧原理提高MCCB的开断性能。

图6-19 模型电流密度分布
a)CB1动、静导电杆电流密度分布 b)CB3动、静导电杆电流密度分布 c)CB1动导电杆和动触头电流密度分布
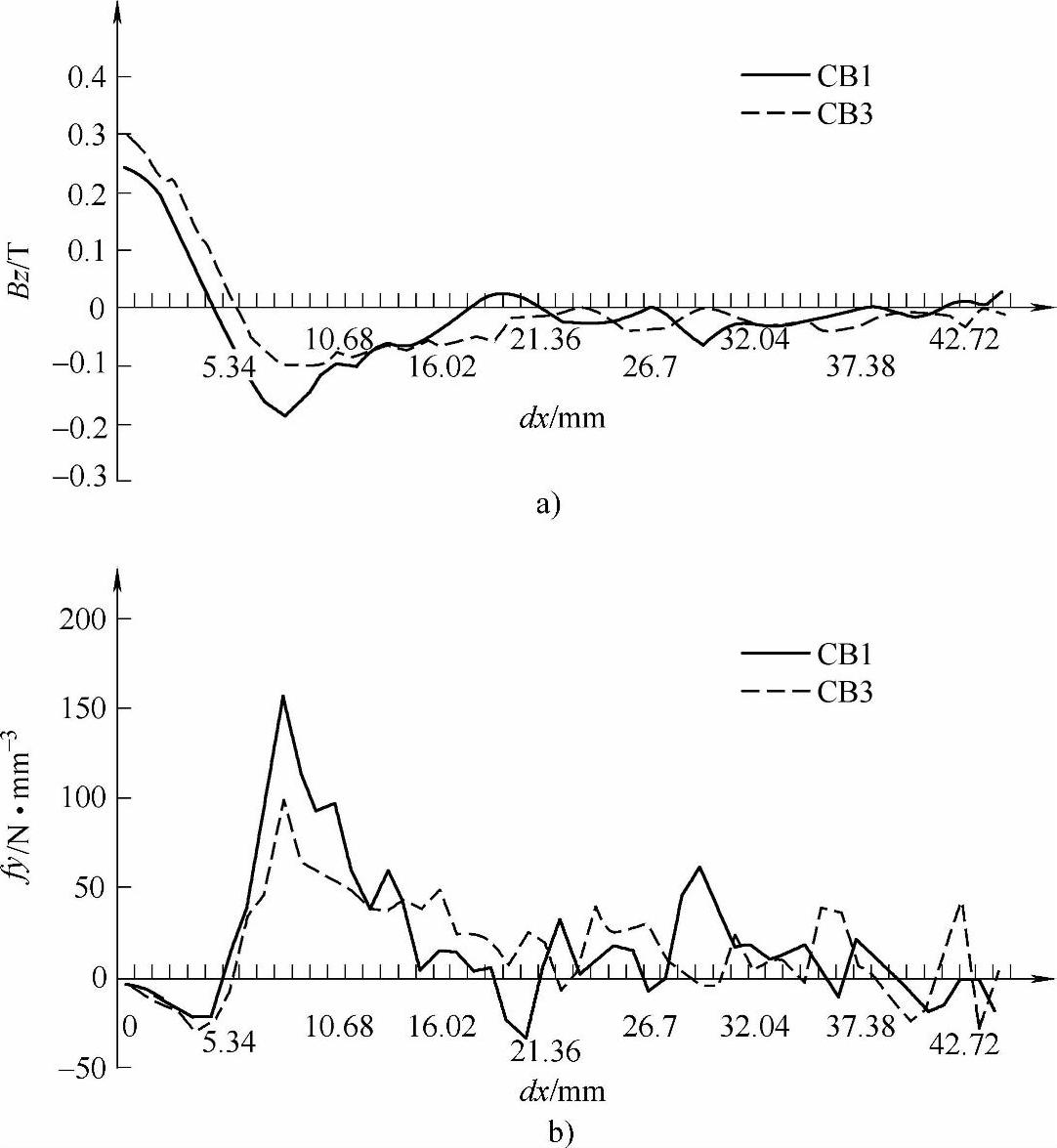
图6-20 CB1和CB3动导电杆上的磁感应强度和力密度分布
a)动导电杆上沿z向磁感应强度分布 b)动导电杆上y方向上力密度分布
表6-3 CB1模型的电流和电动斥力之间的关系

此外,在表6-4所示条件下,可以用Holm公式来计算作用在动触头上的电动斥力FH。对CB1和CB2来说,FH分别为40.33N和38.45N,同表6-4的结果相比,有一定的差别,这主要是由于导电回路产生的磁场对动触头上电动斥力的影响引起的。
表6-4 5个模型在10kA电流时的电动斥力计算结果

有关低压断路器的建模仿真技术的文章

然而,随着颗粒体积分数的增大,炸药的脆性增加,更容易发生拉伸破坏。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。图8-35三种不同颗粒体积分数和颗粒分布细观结构模型的应力-应变曲线图8-36~图8-38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。从三种模型的计算结果可以发现,动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。......
2023-06-27

黄河下游枯、平、丰水年的水沙资源优化配置模型计算方案与历史实测水沙分布比较如表12-9所示。表12-9黄河下游水沙资源优化配置模型计算方案与历史实测水沙分布比较表对于平水年,1986~1999年实测年平均水沙资源分配主要是工农业引水量111.51亿m3、汛期水量92.50亿m3和非汛期水量58.06亿m3,由于引水含沙量较大,下游引水引沙1.116亿t,河槽淤积2.5亿t,河槽严重萎缩,滩区仅淤积0.395亿t,“二级悬河”迅速发展。......
2023-06-23

由于交换设备最先应用于电话网中,所以本小节以电话网为例,讨论交换是如何引入网络的及其作用如何。当距离很远时,汇接交换机也称为长途交换机。用户终端与交换机之间的线路称为用户线,其接口称为用户接口;交换机之间的线路称为中继线,其接口称为网络接口。图4.4中的用户交换机常用于一个集团的内部。当PBX 具有自动交换能力时,又称为PABX。......
2023-06-26

图3-50输送单元的机械手示意图3)拖链装置当机械手装置做往复运动时,连接到机械手装置上的气管和电气连接线也随之运动,机械手装置上的所有气缸连接的气管和电线沿拖链带敷设,插接到电磁阀组上。图3-51输送单元的拖链装置图3-52输送单元的原点开关和极限开关示意图2.输送单元装置侧的安装输送单元装置侧的安装分为两部分:直线运动组件的安装、拖链的安装和机械手装置的安装。图3-54输送单元装置侧安装完成示意图......
2023-06-15

图13-24异重流潜入位置变化过程表13-7水库运用初期1~5年库区输沙计算结果图13-24异重流潜入位置变化过程表13-7水库运用初期1~5年库区输沙计算结果在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明,距坝67km 以下库段总淤积量为29.44 亿m3,若淤积物干容重γ0=1.15t/m3,则淤积量为33.8亿t。......
2023-06-23

我们注意到,单轴拉伸下的失效应变仅为0.004 1,说明PBX 9501 是一种脆性材料。图8-20应变率为10-3s-1时的单轴拉伸应力-应变曲线图8-21 所示为应变为0.16%、0.41%、0.45%和0.5% 时的Y 方向应变云图和损伤断裂演化图。从图中可以看出,整个拉伸过程黏结剂承受了大部分的变形。该结果表明PBX 9501 的拉伸力学性能与界面黏结强度有关,而失效路径与界面强度无关。......
2023-06-27

表5-20 三角试片炉前控制2)快速金相检查法。表5-22 蠕墨铸铁炉前调整补救措施3.浇注后检测蠕墨铸铁浇注后常见检测方法有:断口分析法、音频检测法、超声波速度检测法和金相检测法。......
2023-06-24

随着低速柴油机制造工业的快速发展,新的机型不断出现,气缸体的结构不断发生变化。这种气缸体的造型、制芯等工艺过程较为复杂,生产难度较大,制作成本较高。随着新机型的不断出现,近代柴油机气缸体已由冷却型改为非冷却型,使气缸体的内腔结构大为简化,便于铸造。多联缸体的毛重,则根据气缸体直径大小及连接气缸筒的数量而定。另外,当有局部铸造缺陷和在工作过程中有局部损坏时,单缸体便于更换,从而可减少损失。......
2023-07-02
相关推荐