比较两种U形静触头导电回路的电动斥力与吹弧磁场分析

2023-06-15 百科知识版权反馈

【摘要】：图6-13 平行进线U型静导电杆的电流回路2.计算结果分析触头电动斥力、吹弧磁场是影响断路器开断性能的两个重要指标。下面对两种结构触头闭合时电动斥力、触头打开且电弧燃烧时的吹弧磁场进行对比分析。

1.两种U形静触头导电回路

塑壳断路器的限流作用主要取决于电弧电压U_arc，它由两部分组成，包括电弧拉长后的弧柱压降U₁和近极压降ΔU。根据大量实验显示，近极压降ΔU一般为20～25V左右。塑壳断路器为了提高电弧电压，一般采用栅片灭弧，若栅片数为n，则把长弧分割成n+1个短弧，这样电弧电压可用下式表示：

上式中，i为电弧电流，l为弧柱长度，由于电弧的近极区极短，因而可以认为电弧长度即为l，σ为电弧的电导率，A为电弧的截面积。

因而，对于塑壳断路器，要提高电弧电压U_arc和限流性能，一方面在电弧能顺利地进入栅片的条件下（即要保证栅片之间的间距足够大），尽可能地增加栅片数目n；而另一方面通过拉长电弧和充分冷却弧柱，尽可能提高弧柱压降U₁。

触头区由导电回路产生的自励磁场，与动触头导电杆通过电流相互作用会产生电动力，使动触头尽快斥开，并在电动力作用下，动导电杆快速运动，可使电弧电压提前呈现并快速上升，它作为吹弧磁场又使电弧受到冷却并快速驱动，这些都有利于提高断路器开断性能。

塑壳断路器的静导电杆有一个U型的回路，这是一种很常用的结构，它能使电流在动静触头回路流动时方向相反，采用这种结构与传统的平板式静导电回路相比有两个优点：

1）增加动触头所受的电动斥力。如图6-10所示，图6-10a中静导电杆采用下进线U型结构，由于电流在静导电杆与动导电杆中流向相反，动触头所受到的回路力F_L为向上的斥开的力，加上因电流收缩引起的Holm力F_H，动触头所受的总的电动斥力为F_H+F_L；而图6-10b中静导电杆采用平板型结构，由于电流在动静导电杆中流向相同，动触头所受到的回路力F_L为向下的吸合的力，因而动触头所受的总的电动斥力为F_H-F_L。可以看出U型的静导电杆比传统平板型的静导电杆能对动触头提供更大的电动斥力。

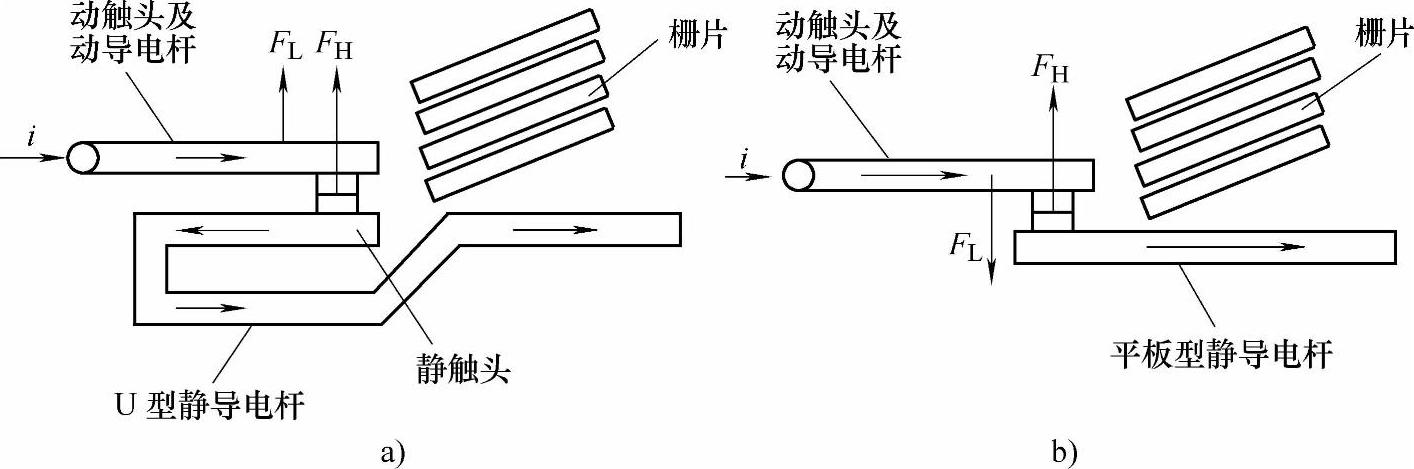
图6-10 两种不同类型静导电杆的动触头电动斥力对比

a）U型静导电杆 b）平板型静导电杆

2）增加电弧向栅片方向的磁吹力。如图6-11所示，图6-11a中静导电杆采用U型结构，当触头导电回路通以电流时，由动导电杆产生的磁场将对电弧提供洛仑兹力F_动，其方向为将电弧向栅片方向推动，而静导电回路对电弧的电动力F_静也同样将电弧推向栅片，所以电弧受到导电回路的磁吹力为F_动+F_静；而图6-11b中静导电杆采用平板型结构，静导电杆对电弧的电动力F_静将电弧向栅片相反的方向推动，此时电弧受到导电回路的磁吹力为F_动-F_静。所以，U型的静导电杆比传统平板型的静导电杆能对电弧提供更大的磁吹力。

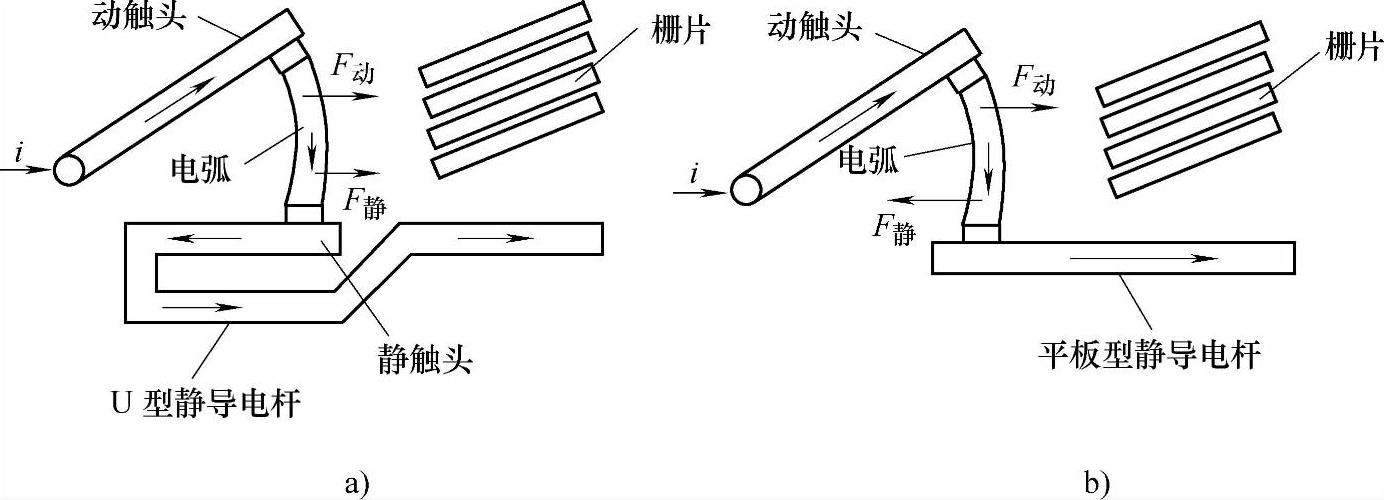
图6-11 两种不同类型静导电杆的电弧磁吹力对比

a）U型静导电杆 b）平板型静导电杆

下进线U型静导电回路虽然比传统的平板型静导电回路能提供更大的触头电动斥力和吹弧力，但它也有缺点，就是占用了灭弧室较大的空间，在断路器高度一定的条件下，会使触头开距变小，放置的栅片数也减少，由式（6-9）可知：这会影响电弧电压的提高。为了减小静导电杆占用的空间，并保留电流在动静触头间流动时方向相反的特征，提出一种平行进线U型静导电杆结构，如图6-12所示，将静导电杆压低，并设置一个带斜坡的导电板来容纳静触头，从而使得在同样断路器高度下，灭弧室能够容纳更多的栅片，并能提高动静触头之间的开距，使电弧被拉得更长。平行进线U型静导电杆的电流回路如图6-13所示，通过静触头导电板的电流与动导电杆方向相反，然后电流在一个平面内分两路平行汇总于一个出线端，平行进线U型静导电杆提供的电动斥力和吹弧力与下进线U型静导电回路相近。

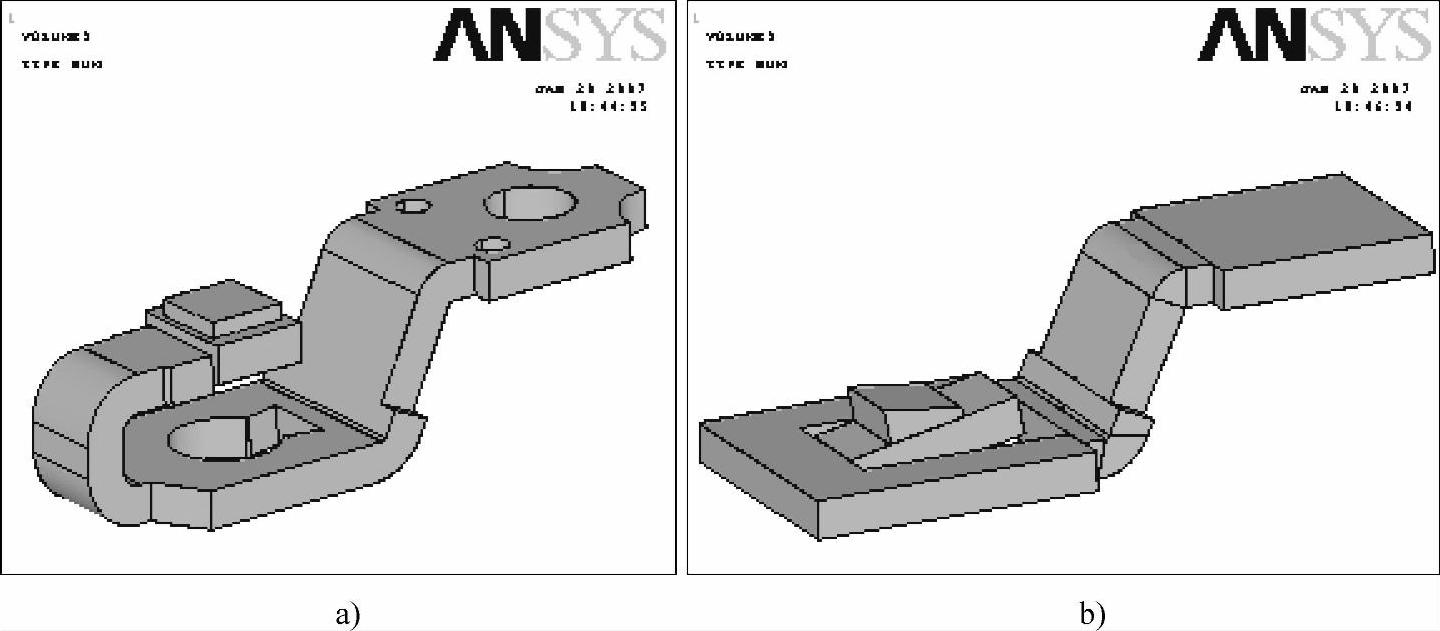
图6-12 两种静导电回路形状对比

a）下进线U型静导杆 b）平行进线U型静导杆

图6-14为两种静导电回路结构的灭弧室的1/2模型，可以看到，在高度相同条件下，平行进线U型静导杆模型比下进线模型增加了栅片，机构开距也增大，使电弧被拉得更长，从而可以提高断路器的熄弧电压和限流特性。

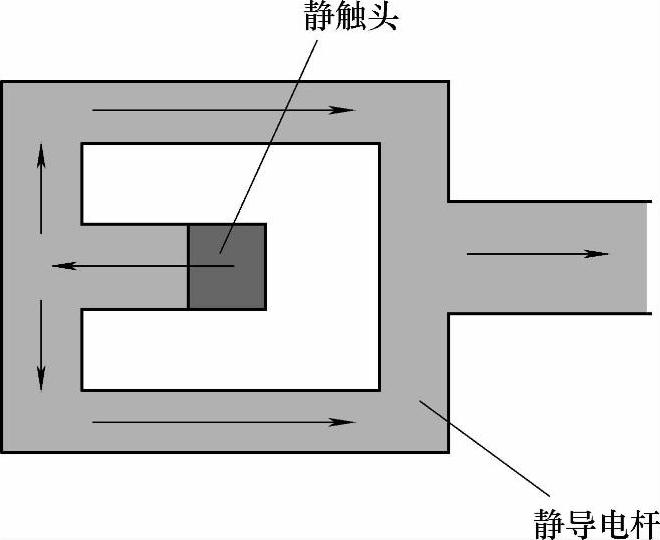
图6-13 平行进线U型静导电杆的电流回路

2.计算结果分析

触头电动斥力、吹弧磁场是影响断路器开断性能的两个重要指标。下面对两种结构触头闭合时电动斥力、触头打开且电弧燃烧时的吹弧磁场进行对比分析。

我们所要计算的电动斥力由两部分组成，包括动导电杆所受的洛伦兹力和动静触头间因电流收缩而产生的Holm力。动导电杆所受的洛伦兹力可以利用下面的公式来计算：

式中 F_L——洛伦兹力；

J_S——电流密度；

B——磁感应强度；

V——体积。

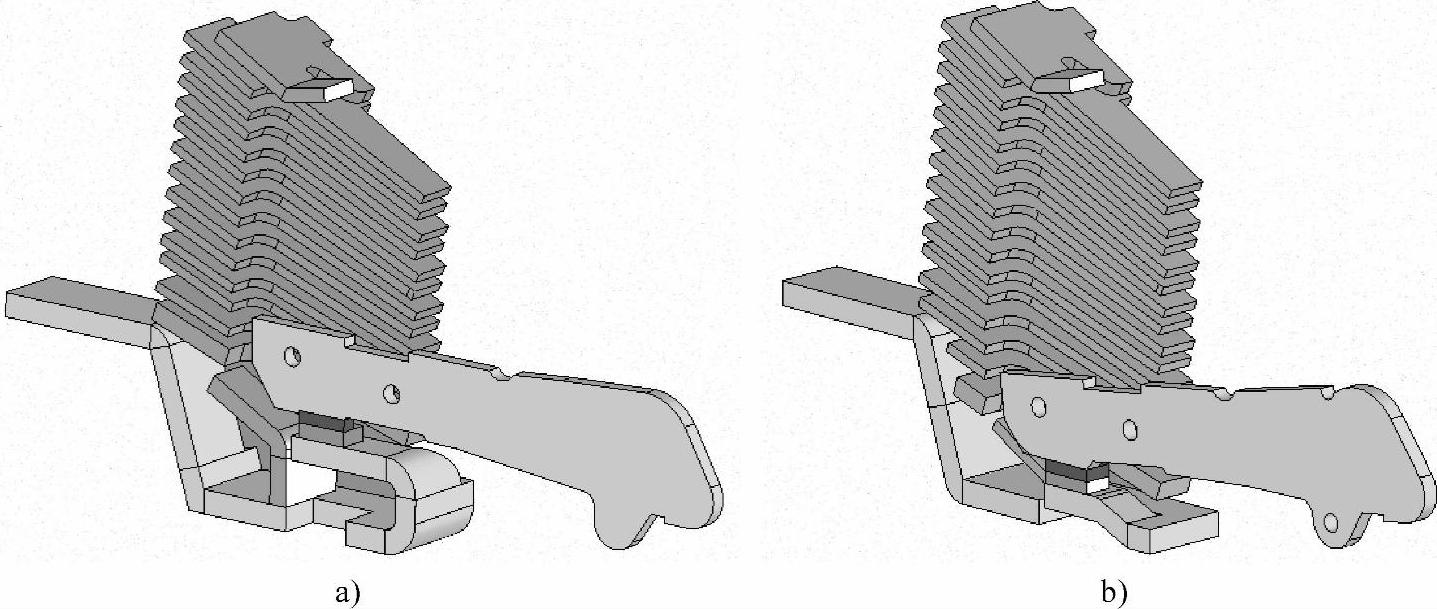
图6-14 两种静导电回路模型对比（1/2）

a）下进线U型静导杆模型 b）平行进线U型静导杆模型

由公式（6-10）可知，要求回路电动斥力F_L，须先求解由动静导电杆和动静触头所组成的载流回路中的电流密度J_S分布，以及灭弧室磁感应强度B的分布。

在宏观环境下，动静触头的面接触仅是在微观下的点接触，由于这个原因，在这些接触点上就会造成电流收缩集中，从而产生Holm力，其本质仍然是电动斥力，该力的计算公式为

式中 F_H——动触头所受Holm力；

μ₀——真空中的磁导率；

A——动静触头之间的接触面积；

ξ——触头接触系数；取值范围为0.3～0.6，通常取0.45；

H——触头材料的布氏硬度，一般取900；

F_K——触头正压力。

为了比较，下面分别计算额定电流为400A塑壳断路器的不同静导电杆的动触头上电动斥力，三种结构分别是下进线U型静导杆、平板型静导杆和平行进线U型静导杆。

图6-15为不同静导杆结构的灭弧室有限元模型，采用上述计算方法，在不同电流下，利用公式（6-10）、（6-11）计算动导电杆所受的围绕其转轴的回路电动斥力矩、归算到动触头中心的回路电动斥力和Holm力，然后将后两者相加，即为所要求解的总电动斥力。所受的总电动斥力数据制成曲线，如图6-16所示。从图中可以看出，平行进线U型静导杆结构的动触头所受电动斥力最大，下进线U型静导杆结构的次之，平行板静导杆的最小。说明平行进线U型结构的静导杆对动触头的快速斥开是有利的。

图6-15 不同静导杆结构的灭弧室有限元模型（1/2）

a）平板型 b）下进线U型 c）平行进线U型

下面对不同静导杆结构下电弧燃烧时的灭弧室模型进行吹弧磁场的对比分析。计算过程依然要分为两步进行，首先进行静态电流传导分析，然后再进行磁场的仿真和计算。本文分析了在通以10kA大小的短路电流时，塑壳断路器在不同静导杆结构下的吹弧磁场。

图6-16 不同静导杆结构时动触头所受电动斥力的对比曲线

首先计算得出三种模型在电流10kA时的整体的磁通分布情况，再来求解电弧中心线上的磁感应强度。将电弧的中心线等分为9段，从而得到10个点，编号从下至上依次为1～10，这10个点形成一条路径，情况和图6-6相似。把三种情况下电弧中心10个点上的磁感应强度罗列出来，并制成了对比曲线，如图6-17所示。

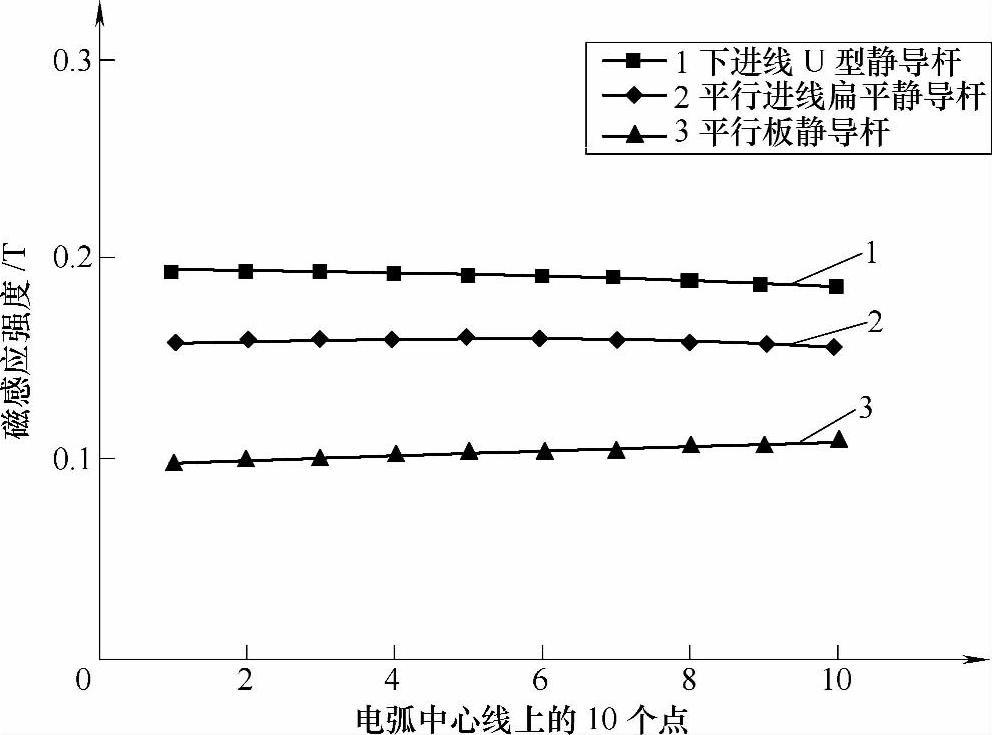
图6-17 三种结构电弧中心线上的磁感应强度对比曲线

可以看到，下进线U型静导杆结构电弧中心线上的吹弧磁场最强，平行进线U型静导杆结构次之，而平板型静导电杆结构吹弧磁场最弱，并与前两者差距较大，采用平行进线U型静导杆结构虽然吹弧磁场小于下进线U型结构，但断路器的开距可增加，电弧被拉得更长，栅片数目可比原来增多，并且由前面分析，它的动触头所受电动斥力是三种结构中最大的，这些都有利于提高断路器的开断性能，因此这种静导电杆结构目前在塑壳断路器中得到广泛的应用。

比较两种U形静触头导电回路的电动斥力与吹弧磁场分析

相关推荐