计算方法及步骤优化

2025-09-29 百科知识版权反馈

【摘要】：近年来，人们将有限元方法和积分方程法应用到电动斥力的数值计算中。采用三维有限元方法计算作用在动导电杆上的Lorentz力，已在2.3.2节中予以详细说明。如2.3.2节中所述，触头的接触表面由形状各异的导电斑点组成。表6-1和表6-2分别为计算条件和计算结果。可以发现，高度h在0.1～0.25mm之间变化时，电动斥力数值变化不大。因此，在下面的计算中，导电桥高度h均设定为0.2mm。

一般来说，看似平坦光滑的触头表面其实是凹凸不平的，而且覆盖有一层不导电的氧化层。不同的触头材料、不同的加工方法、不同工艺过程所得到的表面微观状态都不相同，它将在很大程度上影响两金属表面相互接触的物理过程和接触表面的物理图景。而在触头压力弹簧的作用下，触头表面将发生塑性变形，绝缘膜破裂后形成分布的尺寸各异的微小导电斑点，从而组成为触头的接触表面。Holm是电接触领域的开拓者和奠基人，并提出了著名的Holm公式。

近年来，人们将有限元方法和积分方程法应用到电动斥力的数值计算中。采用三维有限元方法计算作用在动导电杆上的Lorentz力，已在2.3.2节中予以详细说明。这里重点介绍引入导电桥模型来模拟触头间的电流收缩，如何统一计算作用在动导电杆上的电动斥力。

如2.3.2节中所述，触头的接触表面由形状各异的导电斑点组成。这样当电流流过触头时，电流线在接触面附近发生收缩，因而在触头间会产生电动斥力，也即Holm力F_H。一般来说，它与电流瞬时数值i，触头间的预压力F_K，触头材料的布氏硬度H，触头形状及触头表面的导电斑点分布情况等有关。可以用式（6-8）所示的Holm公式来描述。其中r为导电斑点的半径，R为触头的等效半径，ξ用来表征触头的表面接触情况，其范围为0.3～0.6，一般取0.45。

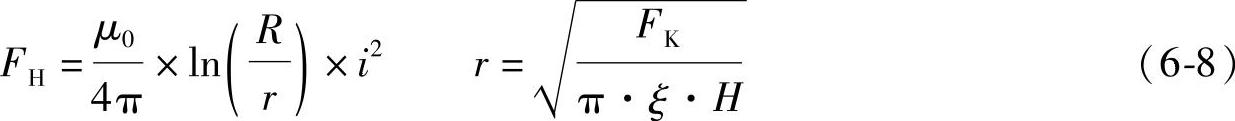
对于Holm公式的一般工程应用来说，假定接触面中心只有一个导电斑点，或者认为全部的导电斑点集中在中心形成一个大的导电斑点。因此，可以用所谓的导电桥模型来模拟触头间的电流收缩，图6-9为导电桥模型的示意图。导电桥材料属性和触头相同，接触半径r可用式（6-8）得到，其高度参数可采用上述方法，过一对孤立触头的电动斥力计算来确定。表6-1和表6-2分别为计算条件和计算结果。可以发现，高度h在0.1～0.25mm之间变化时，电动斥力数值变化不大。因此，在下面的计算中，导电桥高度h均设定为0.2mm。

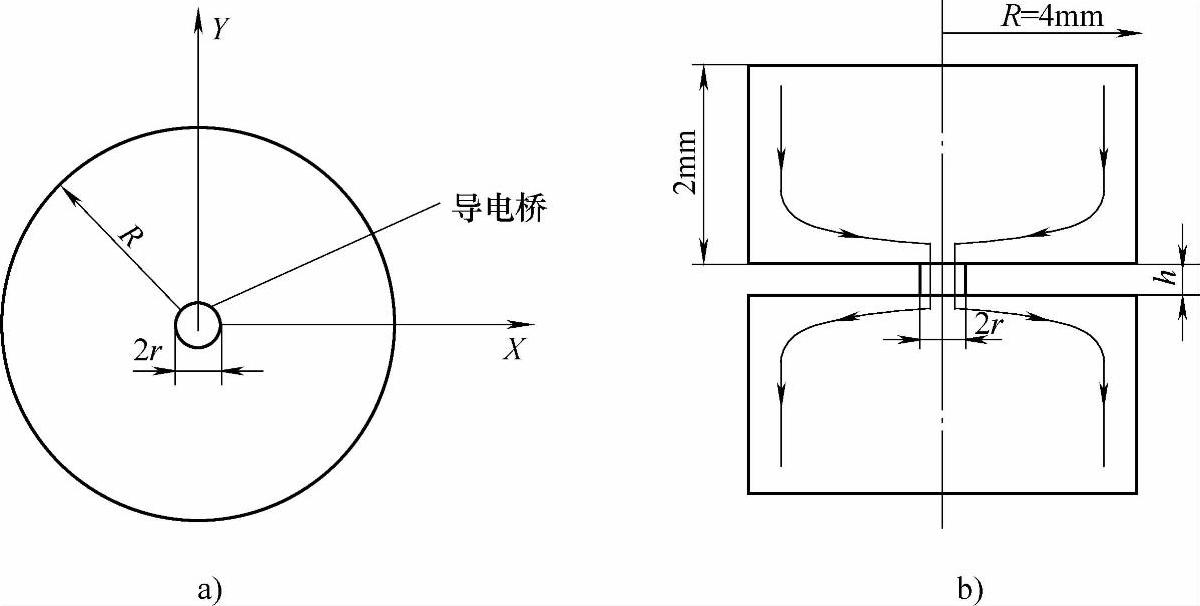
图6-9 导电桥模型示意图(https://www.chuimin.cn)

a）正视图 b）前视图

表6-1 仿真条件

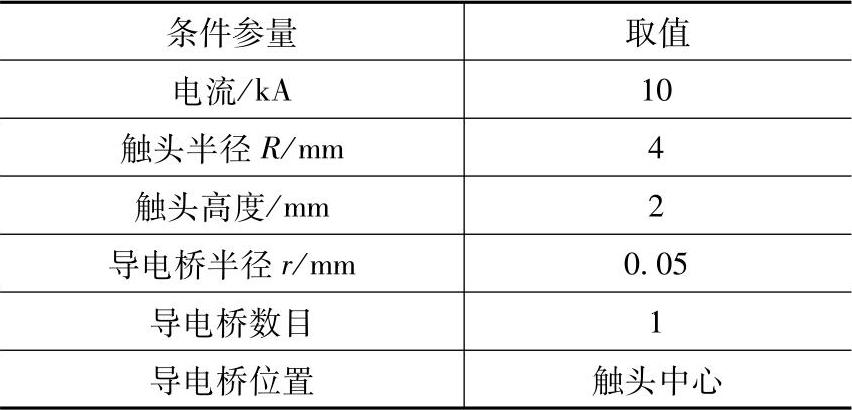
表6-2 一对孤立触头间的电动斥力分析

计算方法及步骤优化

相关推荐