【摘要】:利用Ansys E-mag和Ansys CFX进行电-磁-热-流序贯耦合分析的典型步骤如图5-19所示。由于本节将断路器简化为三导体模型,故利用真实断路器内导体表面积与三导体模型中导体表面积之比,将这一等效热导率修正为0.156W·m-1·K-1,赋予三导体断路器模型中的等效散热介质。开关柜电磁耦合模型如图5-21所示,导电回路居中,其他部件的相对磁导率与空气相差不大,故未予区分,并建为半球形。
典型的三相配电开关柜模型如图5-18所示,其内部主要安装有4个双断点塑壳断路器。两个额定电流为630A的进线断路器位于左侧,并通过铜箔软连接与母线转接器连接,其中最左侧的为备用进线断路器;两个额定电流为400A的出线断路器位于右侧,并通过圆柱导体与母线转接器连接。母线转接器分别挂在三相母线上,三相母线固定在绝缘背板上。开关柜的柜顶设有六组出气口,每组含4个矩形出气口。对应地,柜底设有六组进气口。
利用Ansys E-mag和Ansys CFX进行电-磁-热-流序贯耦合分析的典型步骤如图5-19所示。首先,利用Ansys E-mag模块,考虑涡流和邻近效应,通过三维电磁谐波分析获得导体内部焦耳生热分布;其次,将随坐标变化的焦耳生热功率数据以.csv文件格式导入Ansys CFX模块中,作为热源;最后,利用瞬态计算流体力学方法,进行开关柜温升仿真,获得流速和温度分布等结果。
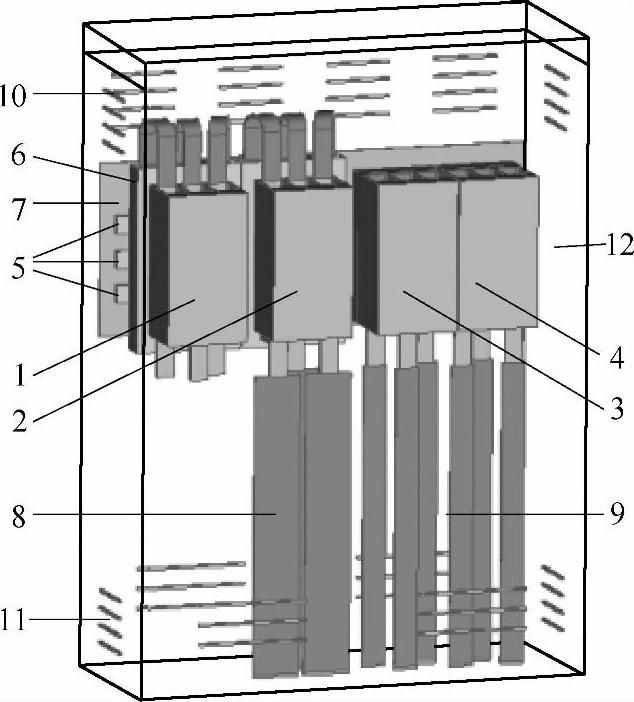
图5-18 低压配电柜模型
1—备用断路器 2—进线断路器 3—第一出线断路器 4—第二出线断路器 5—三相母排 6—维纳尔转接器 7—母排固定覆板 8—三相进线铜排 9—三相出线铜排 10—出气口 11—进气口 12—配电柜外壳
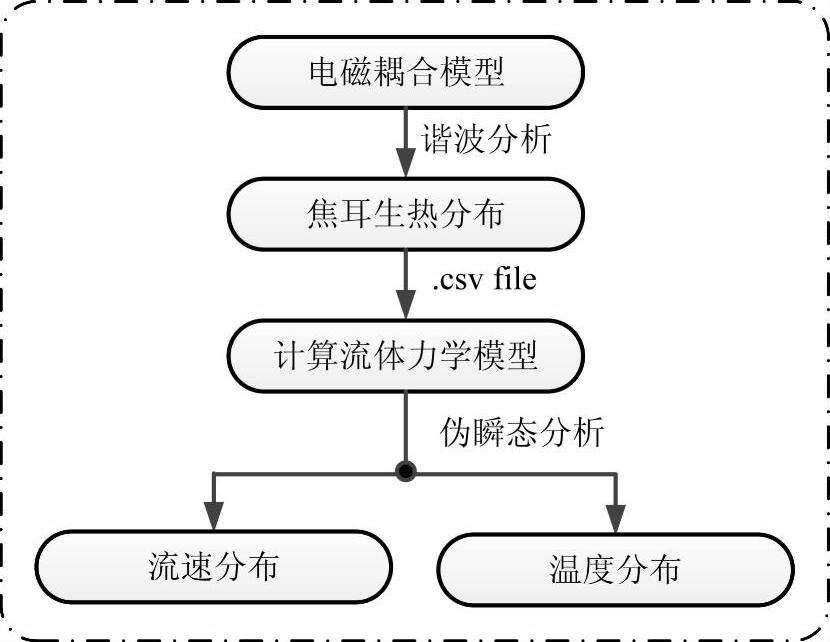
图5-19 电磁热流耦合仿真流程图
1.开关柜发热功率的计算方法
断路器内部的温升分布不是本节的研究重点,且其内部零部件较多,故本节基于生热与散热功率守恒将其简化为三平行导体模型,如图5-20所示。其中,每相导体在对应高度上建有两个0.5mm厚的导电接触层用以考虑接触电阻与接触热阻,断路器模型内等效导体和接触层的电阻率与热导率分别通过求解电阻公式(5-51)与魏德曼弗朗兹公式(5-52)获得。

其中ρe和λc分别为电阻率与热导率,Re为实验测得电阻;s和l分别为模型中对应部位的横截面积与高度;L洛伦兹系数,其值取2.4E-8(V/K)2;T为热力学温度。
Frei模型[4]中,双断点塑壳断路器操作机构的等效热导率通过质量平均其内部组件和空气热导率来获得,其值为0.1W·m-1·K-1。由于本节将断路器简化为三导体模型,故利用真实断路器内导体表面积与三导体模型中导体表面积之比,将这一等效热导率修正为0.156W·m-1·K-1,赋予三导体断路器模型中的等效散热介质。
开关柜电磁耦合模型如图5-21所示,导电回路居中,其他部件的相对磁导率与空气相差不大,故未予区分,并建为半球形。计算区域的表面设置磁场通量为零,三相出线端子电压也设为零,三相进线端子分别耦合电压,再以复数形式施加三相交流电流。
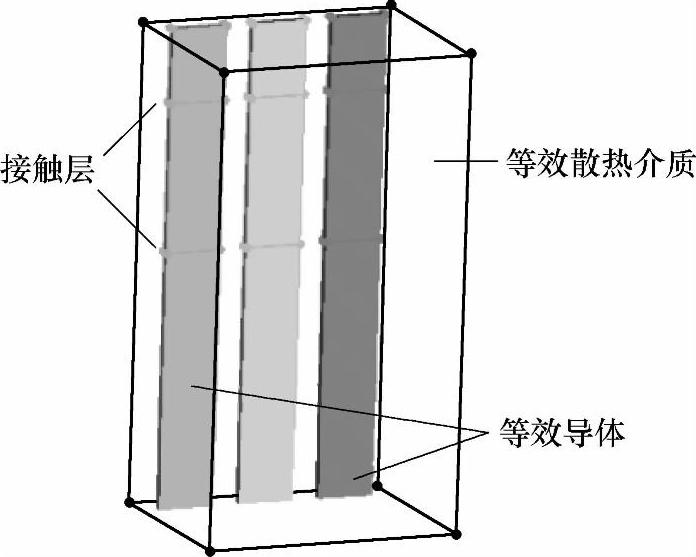
图5-20 简化断路器几何模型
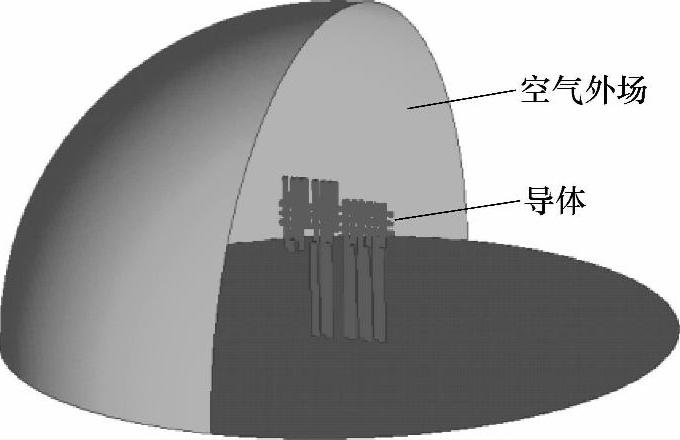
图5-21 导体发热功率计算模型
导体发热功率分布的计算是基于麦克斯韦方程组来计算的,方程的微分形式表示如下:

导体发热功率分布计算主要求解似稳电磁场,求解时可以忽略电场变化产生磁场的影响,即忽略方程中的电通密度。计及辅助方程J=σE和B=μH,得到求解导体发热功率的简化方程组:
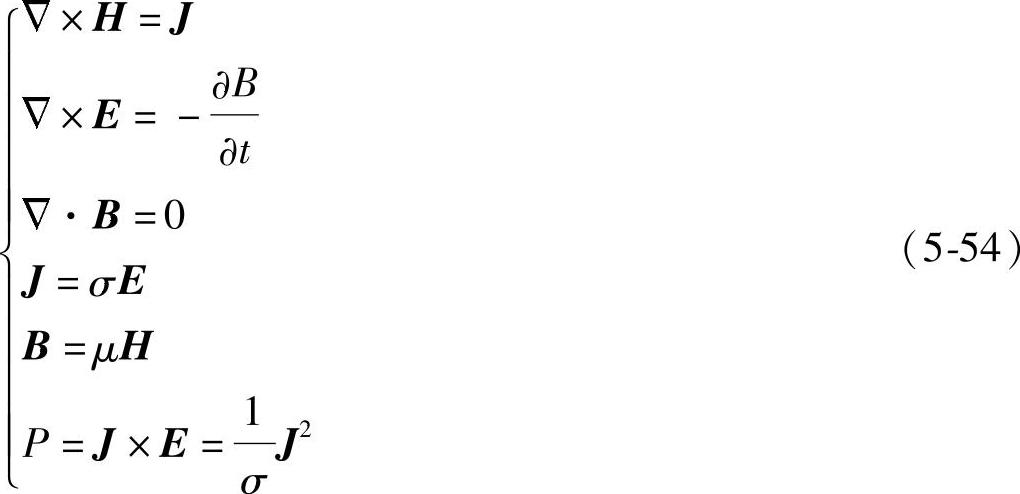
式中 H——磁场强度矢量;
D——电位移矢量;
J——电流密度矢量;
E——电场强度矢量;
B——磁感应强度矢量;
t——时间;
ρ——自由电荷密度;
μ——磁导率;
σ——电导率;
P——焦耳发热功率。
2.开关柜气流温度场的计算方法
开关柜气流温度场模型如图5-22所示,由于开关柜出气口和进气口的流速和压力未知,故将柜外空气也纳入到计算模型中,其中柜外空气的上边界离柜顶约两倍的开关柜高度。计算模型的上边界和四周压力设置为1atm,下边界设置为壁面,此外整个计算域外表面的温度设置为室温283K。
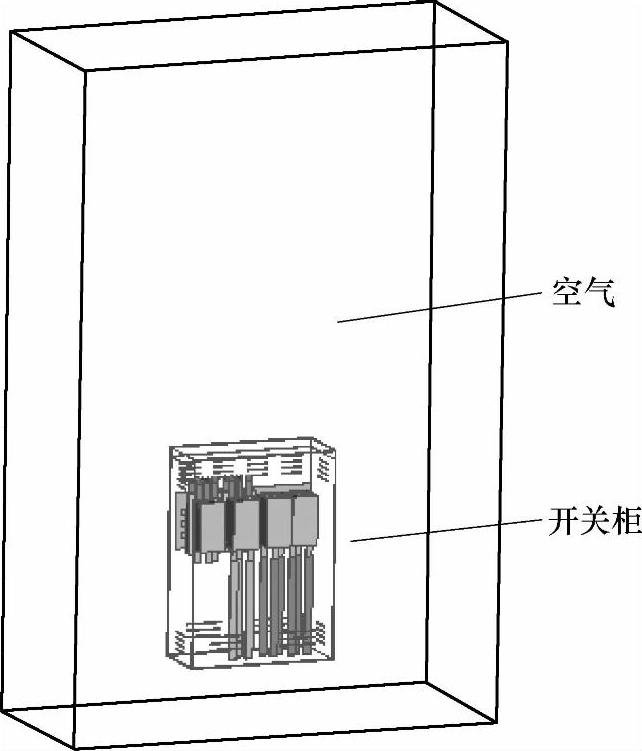
图5-22 开关柜自然对流散热仿真模型(https://www.chuimin.cn)
气流场方程是由质量、动量、能量三个方程所组成:
1)质量守恒方程

式中 ρ——气体密度;
t——时间;
v——气体流速。
2)动量守恒方程
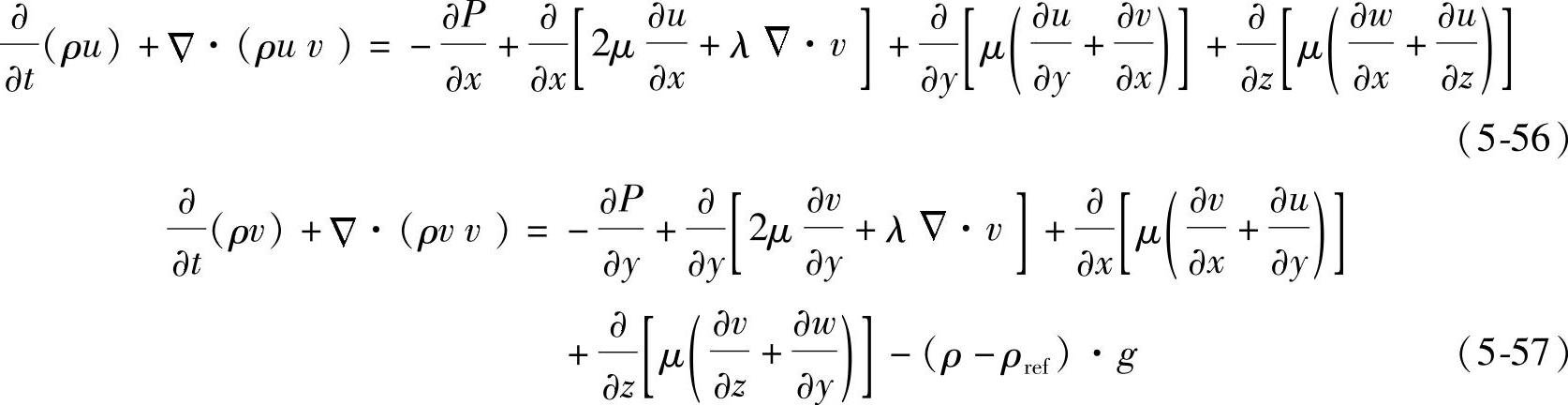
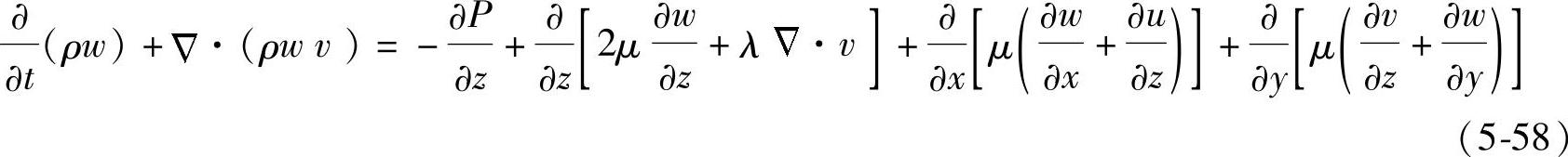
式中 u、v、w——速度分量;
x、y、z——坐标分量;
P——气体压力;
λ——导热系数;
μ——粘度;
g——重力加速度;
ρref——环境温度下空气密度。
在利用Ansys CFX来进行低压配电柜温升仿真过程中,忽略静态气压梯度力,利用Boussinesq近似来考虑浮力,Y方向动量方程中添加随密度变化的源项-(ρ-ρref)·g。
3)能量方程
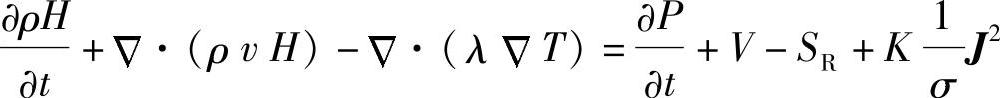
(5-59)(需要修改方程)
式中 H——动态焓;
T——温度;
V——粘性耗散函数;
SR——辐射分量。
由于温升实验中电流有效值恒定,假定电流有效值分布不随温度变化,故在计算温度对生热功率分布的影响时,主要考虑了温度对电阻率的影响。因此,在能量方程中添加随温度变化的源项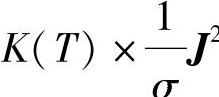 ,考虑电阻率随温度变化对温升结果的影响,其中K(T)为电阻率温度系数,其值随温度变化,等于不同温度下电阻率与室温电阻率的比值。除此之外,能量方程中还加入了辐射分量SR。热辐射模型采用的是黑体辐射模型,方程如下式(5-41)所示:
,考虑电阻率随温度变化对温升结果的影响,其中K(T)为电阻率温度系数,其值随温度变化,等于不同温度下电阻率与室温电阻率的比值。除此之外,能量方程中还加入了辐射分量SR。热辐射模型采用的是黑体辐射模型,方程如下式(5-41)所示:
SR=εk(T4-T40) (5-60)
式中 ε——发射率;
T0——环境温度;
k——玻尔兹曼常数,k=5.67·10-8W·m-2·K-4。
此外,开关柜还通过接线端子向外部导体传热。忽略了外接导线温升对外部空气流动的影响,故模型中未建立外接导线模型,通过求解下述方程获得接线端子向外接导线传递的热流密度:
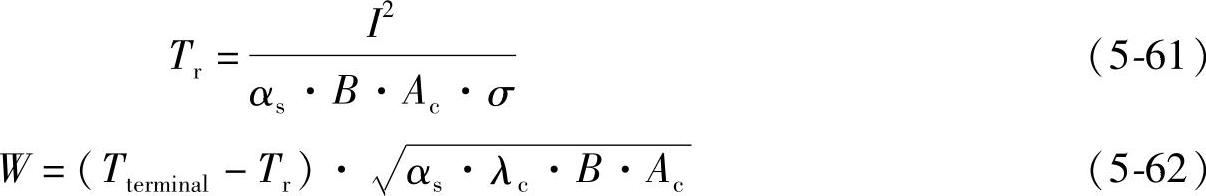
其中,Tr为无限远处的外接导线仅由欧姆加热产生的温升,I为电流有效值,as为外接导线表面对流散热系数(7W/m2·K)和等效辐射散热系数(5W/m2·K)之和,W为接线端子向外接导线传热功率,Tterminal为接线端子处的温升,B,Ac,σ和λc分别为外接端子截面周长、截面积、电导率和热导率。
设定的收敛准则有:1)残差小于10-5;2)全局不平衡度小于1%。当这两个准则都已达到,才认为达到收敛,一般需要500~1000次迭代达到上述收敛准则,具体迭代次数受初值影响较大。







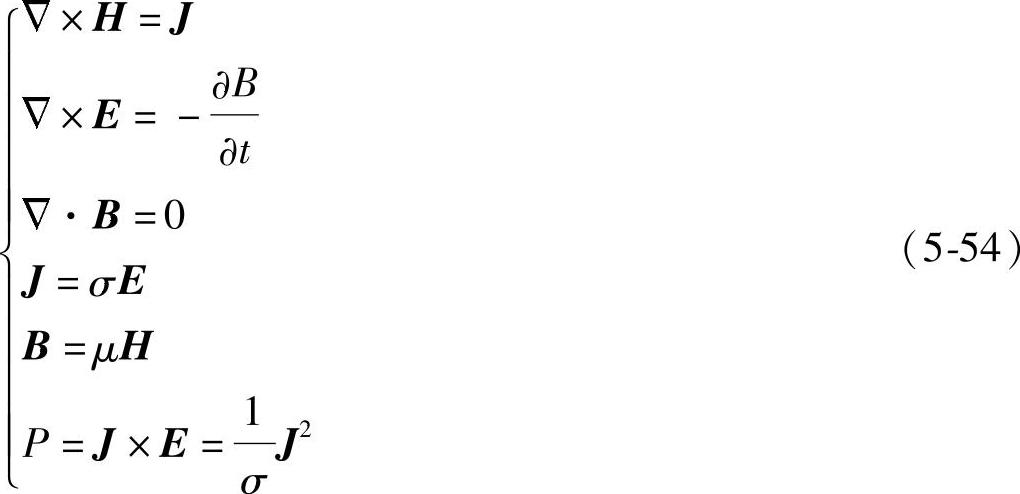


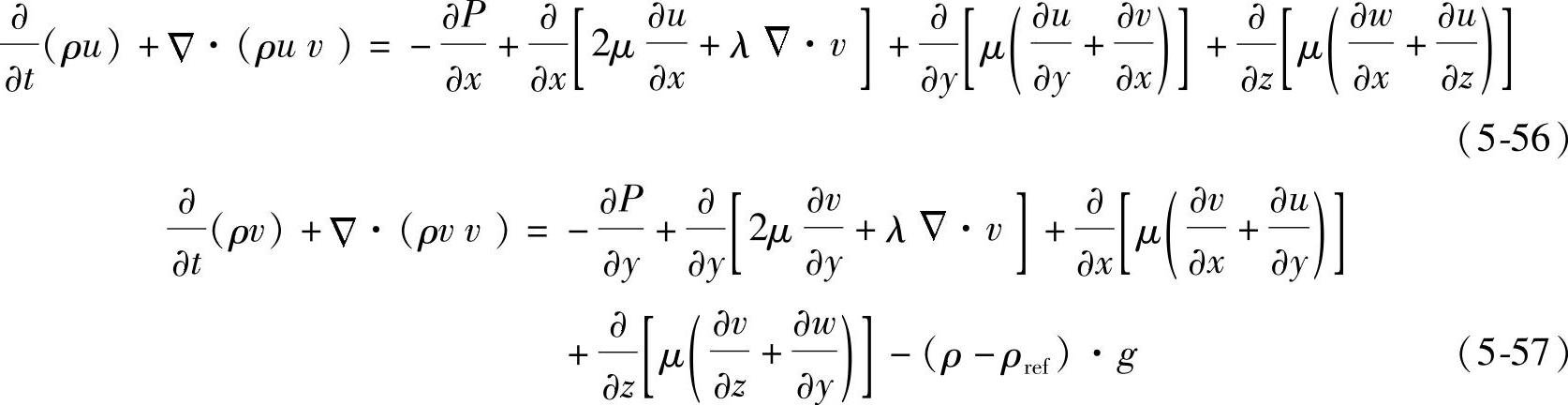
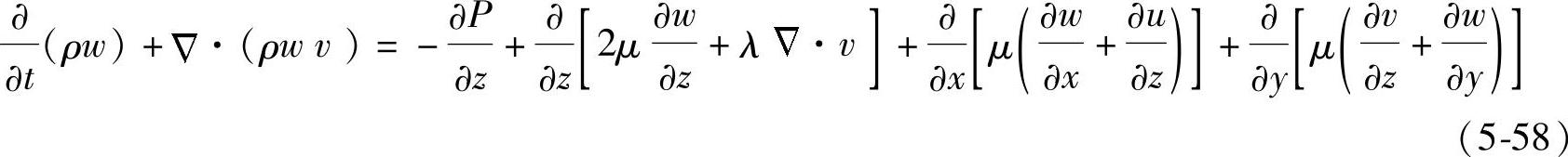
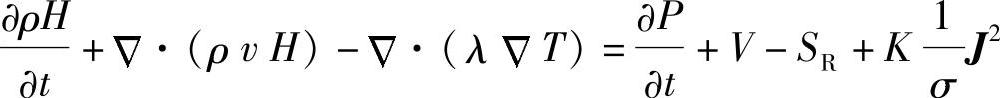
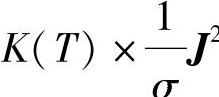 ,考虑电阻率随温度变化对温升结果的影响,其中
,考虑电阻率随温度变化对温升结果的影响,其中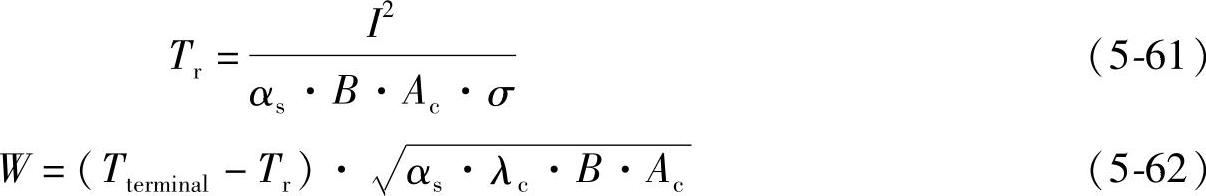





相关推荐