GB 16899—2011对自动扶梯在空载和有载向下运行时的制停距离有相关规定，见表1-5-4。自动扶梯在制停时，人员在惯性的作用下会顺着运行方向前倾，这在向下运行时容易使人员失稳，因此GB 16899—2011中增加了对向下运行时的制停减速要求。GB 16899—2011规定的允许最大正偏差为2%。......
2025-09-29
连接导线的规范与要求
【摘要】：开关电器的温升考核，按国标GB/T14048.1和IEC60947标准规定，试验中把所有极串联起来用单相电流进行试验，但其连接导线必须符合标准的规定。对于试验电流不大于450A的连接导线应采用单芯聚氯乙烯绝缘铜线，连接导线截面积决定于电流大小，例如100A的断路器，要求截面积为35mm2，250A则需150mm2，400A为240mm2。两个接线端连接导线长度，当截面积为35mm2及以下，其长度不小于1m；截面积大于35mm2，则长度应不小于2m。求出Q，连接导线就可作为第二类边界条件来处理。
开关电器的温升考核，按国标GB/T14048.1和IEC60947标准规定，试验中把所有极串联起来用单相电流进行试验，但其连接导线必须符合标准的规定。对于试验电流不大于450A的连接导线应采用单芯聚氯乙烯（PCV）绝缘铜线，连接导线截面积决定于电流大小，例如100A的断路器，要求截面积为35mm2，250A则需150mm2，400A为240mm2。两个接线端连接导线长度，当截面积为35mm2及以下，其长度不小于1m；截面积大于35mm2，则长度应不小于2m。当电流超过400A时，在按标准规定需采用铜排或电缆。
由于连接导线本身要有电阻损耗，会发热，而由接线端传入连接导线的热量也可通过连接导线表面散热，所以它对低压开关电器的热分析起着很重要的作用，计算连接导线的传热和散热，可把连接导线的作用当成边界条件来处理。按热分析的第二类边界条件，即接线端导入连接导线的热流密度为已知，由公式（5-4），由于接线导线的截面积Ac已知，因而上述条件也可转变为已知导入连接导线的热量Q：
Q=Acq （5-26）
导入连接导线的热量Q的求取如下：
连接导线处于空气中，通过对流和辐射散热。对流系数与导线直径和周围环境温度有关。根据文献[5-2]，裸导线的对流散热系数为式（5-27）所示：
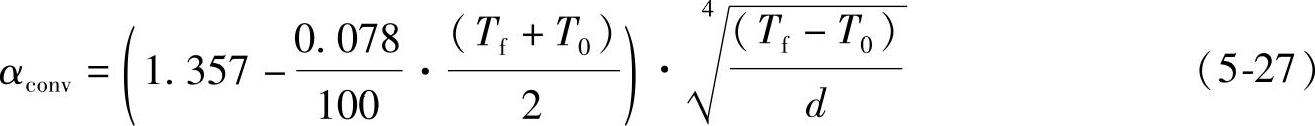
式中 d——连接导线直径（m）。
导线辐射散热系数αrad根据式（5-24）、式（5-25）计算。因此，导线的总散热系数为α=αconv+αrad，同时，导线中通过电流，因此产生焦耳热，自身温度升高，电流I通过导线时由自身的焦耳热引起的导线温升ΔTr为
式中 α——导线的散热系数（W·m-2·K-1）；
B——导线截面周长（m）；
Ac——导线截面积（m2）；
σ——导线的电导率（Ω-1·m-1）。
根据IEC60943和国标GB/T 14048.1—2000规定，对于额定电流小于1000A的三相电器可以将各级串联，用单相电源进行试验。因此，连接导线与接线端的示意图如图5-5所示，为了便于分析设导线材料为匀质裸导线。
设接线端比裸导线温度高ΔT0，裸导线长度为l，温度达到稳定，根据傅里叶定律列出微元dx段的导热微分方程，如式（5-29）所示：
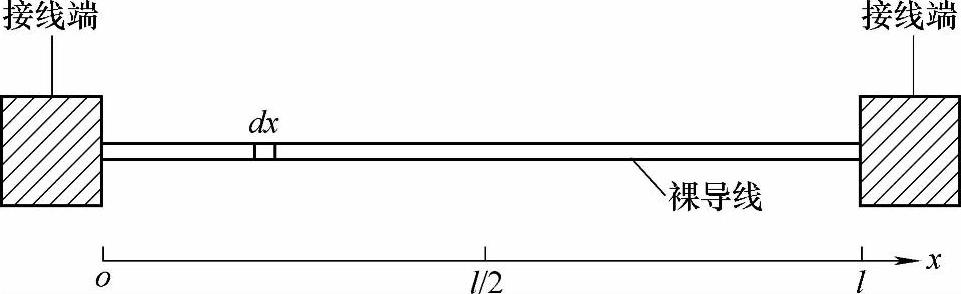
图5-5 接线端和连接导线示意图
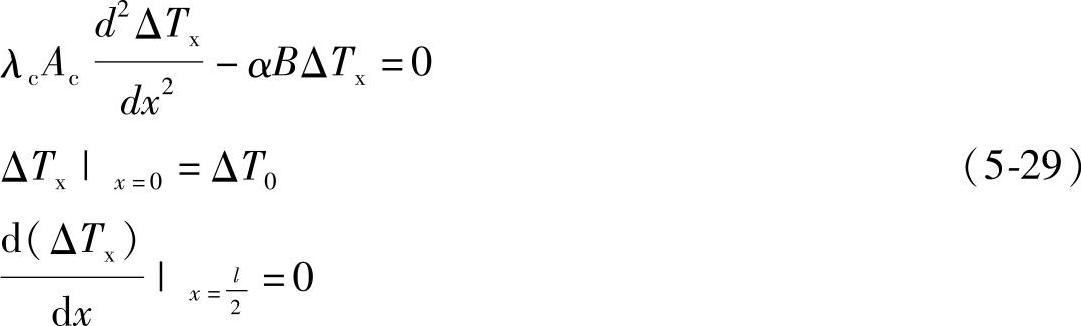
求解得到：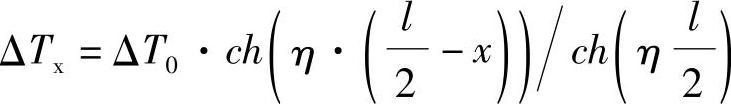
其中：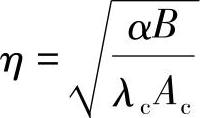
从接线端流入导线的热量为
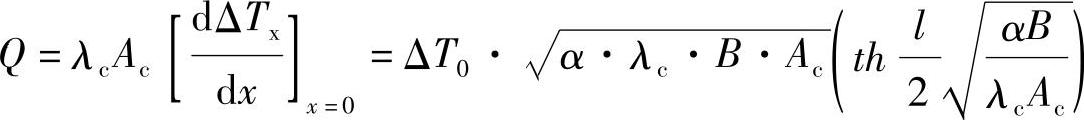
当l→∞时， 
(https://www.chuimin.cn)
当裸导线外面包有绝缘材料时，表面的散热系数会因为绝缘材料的热阻减小，为了用上述的方法计算接线端流入导线的热量，需要对表面散热系数进行处理，连接导线截面积示意图如图5-6所示。
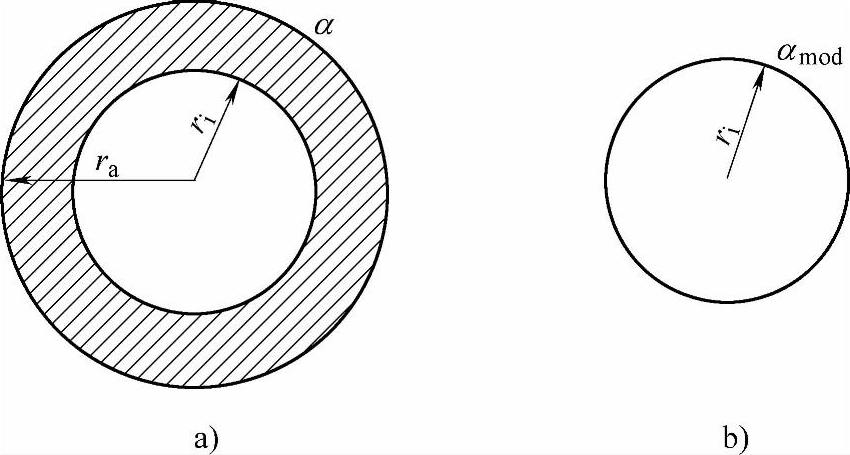
图5-6 导线截面积示意图
a）外包绝缘导线 b）均质材料导线
图5-6a为外包绝缘的导线，阴影部分为导线的外包绝缘，导热系数为λiso。图5-6b为均匀材质的导线。要将图5-6a转换成图5-6b所示的均匀材质的导线，需要将散热系数α转换成αmod。利用热阻分析法可以得式（5-31）：
因此
式中 ra——外包绝缘的导线的半径（m）；
ri——裸导线的半径（m）；
λiso——绝缘材料的热导率（W·m-1·K-1）。
故从接线端流入导线的热量为
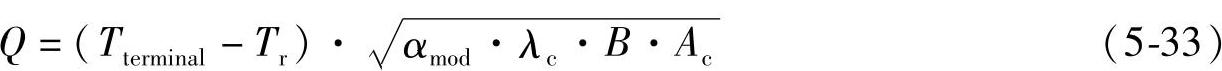
式中 Tterminal——接线端的温度（℃）；
Tr——导线的温度（℃）；
αmod——导线散热系数（W·m-2·K-1）；
B——导体截面周长（m）；
Ac——导体截面积（m2）；
λc——导体的热导率（W·m-1·K-1）。
求出Q，连接导线就可作为第二类边界条件来处理。
相关文章
- 详细阅读
-
控制柜设计规范：电源放置和防护等级要求详细阅读
2）微机的3.3V、5V电源应尽量靠近控制板。除了在控制柜增加风扇，还可以考虑在机房增加风扇，加强散热效果。对于室外型的自动扶梯，为了保证防水，控制柜的防护等级要求达到IP55。......
2025-09-29
-
电线电缆的技术要求详解详细阅读
对于抗干扰要求比较高的信号线，一般使用屏蔽电缆，为进一步提高抗干扰效果，大多数的屏蔽电缆内部都是双绞线方式布置。对于普通的商用项目，一般信号线使用普通的PVC电缆就可以了，但是串行通信线要使用屏蔽双绞线。对于公共交通型自动扶梯项目，一般信号线要使用低烟无卤电缆，对于需要特别防护的地方还要使用铠装电缆，如维修操纵开关盒。电缆是自动扶梯的重要组成部分，设计时要根据使用场合、信号特点及电流大小等仔细确认。......
2025-09-29
-
电气连接线的表示方法详细阅读
电气连接线简称导线，用于连接电气元件和设备，其功能是传输电能或传递电信号。图1-16 导线特征表示举例图1-17 导线换位表示举例图1-18 导线连接点表示举例3.导线连接关系表示导线的连接关系有连续表示法和中断表示法。导线连接的中断表示如图1-21所示，图1-21a采用在导线中断处加相同的标记来表示导线连接关系，图1-21b采用在导线中断处加连接目标的标记来表示导线连接关系。......
2025-09-29
-
自动扶梯扶手的强度要求详细阅读
为保证乘客搭乘自动扶梯的安全性，扶手装置的强度也需要达到如下的强度要求：1.承受外力能力扶手装置应能同时承受静态600N的侧向力和730N的垂直力，这两个力均匀分布在扶手带导向系统顶部同一位置1m的长度上。测试承受外力能力、护壁板刚度和围裙板刚度时的加载部位如图6-1-4所示。......
2025-09-29
- 详细阅读
- 详细阅读
-
提高抓取精度的方法和要求详细阅读
原则上，每个自动化工序都有不同的精度要求。在这种情况下，工件位置不再精确地集中在手指之间，这可能导致连接操作中的精度问题。由于对抓取或放置精度的要求如此之高，因此应相应地调整一般条件，以避免此类错误。图3.117用公差角度来审视系统对于抓取或者放置来说十分重要摄像机测量误差可能具有不同的性质。当涉及在装配过程中对工件的纯搬运时，或如图3.117所示，当相当多的因素影响精度时，这些考虑尤其重要。......
2025-09-29
相关推荐