图1-12 车刀切削部分的结构要素2.刀具的几何参数刀具静止参考系的各平面如图1-13所示。影响刀具合理几何参数选择的主要因素是工件材料、刀具材料及类型、切削用量、工艺系统刚度以及机床功率等。......
2023-06-26
脱扣器几何参数优化设计
【摘要】：作为短路保护的电磁脱扣器对断路器的短路开断过程有重要作用，它的动作时间越短，越有利于提高短路开断性能，对塑壳断路器来说，更有利于达到操作机构动作与触头斥开过程的合理配合，防止动触头斥开后的跌落现象。所以实现电磁脱扣器的优化设计，一般可取动作时间最短作为优化的目标，而把几何尺寸作为设计变量。
作为短路保护的电磁脱扣器对断路器的短路开断过程有重要作用，它的动作时间越短，越有利于提高短路开断性能，对塑壳断路器来说，更有利于达到操作机构动作与触头斥开过程的合理配合，防止动触头斥开后的跌落现象。所以实现电磁脱扣器的优化设计，一般可取动作时间最短作为优化的目标，而把几何尺寸作为设计变量。
关于电磁脱扣器的保护性能计算已在上面几节中叙述，计算方法是耦合三相有限元电流场和磁场分析，优化设计需要进行大量设计方案寻优计算，若采用三维有限元方法计算其电磁特性，则工作量太大，这里采用4.3节同样的方法，基于三维磁场分析，建立等值磁路，然后用磁路方法进行优化设计，这样既保证了计算准确性，又能大幅度减少计算工作量。
图4-27显示了分析对象的模型和它的有限元剖分，由于分析对象的截面左右对称，所以图上只显示了一半，图4-28是三维磁场计算结果，然后利用图4-28的磁场分布，组成如图4-29所示的等值磁路，图中IN是磁路的磁势，对照图4-30的尺寸图，G1是铁轭底部的磁导，G2和G3是铁轭两边两个截面不同部分的磁导，Gδ1、Gδ2和Gδ3是铁轭两侧边三个不同部分间气隙的漏磁导，Gδ是工作气隙磁导，G5是衔铁顶部的磁导，Gδ4是衔铁两侧边间空气隙的漏磁导，气隙磁导的计算对计算准确性影响最大，其计算公式如下：
式中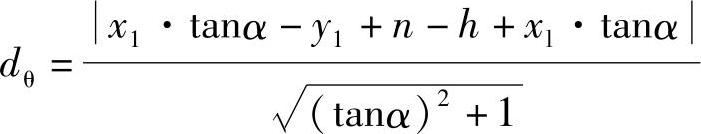
k1=0.87（1+sinθ）（表征衔铁侧板两端漏磁导随气隙变化的拟合量）；
k2=0.81（表征铁轭侧板第一段漏磁通有效截面积的拟合量）；
k3=0.88（表征铁轭侧板第一段漏磁通有效截面积的拟合量）；
k4=0.92（表征铁轭侧板第一段漏磁通有效截面积的拟合量）；
k5=0.93（表征衔铁侧板漏磁通有效截面积的拟合量）；
μ0——空气绝对磁导率；
图4-30所示为上面式中各变量的定义。
图4-27 磁脱扣器的剖分模型
图4-28 脱扣器的空间磁场分布（不含空气）
图4-29 磁脱扣器的等值磁路
图4-30 磁脱扣器的尺寸图
利用上述等值磁路，可计算出磁脱扣器的静特性，即电磁转矩M和磁系统磁链ψ与衔铁转角θ和通过电流i的关系：
式中 lg——衔铁力臂；
δ——归化到衔铁受力点的气隙。
计算求得的M和ψ，可列成数据网络，耦合电路瞬态和机械运动方程，即可用龙格-库塔（Runge-Kutta）法求得磁脱扣器的动特性，包括脱扣器的动作时间t。
根据对磁脱扣器的要求，可列出优化设计的数学模型
Mint=f（n，l，h，a，m，d，wx） （4-23）
式中设计变量n，l，h，a，m，d，wx是脱扣器的几何尺寸，见图4-30所标，优化设计的约束条件按工艺和结构要求取这些变量的上下限。脱扣器的反力特性是给定的，反力弹簧的初始力矩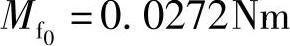
，刚度系数k=0.026Nm/rad。通过优化设计，当脱扣器通过4kA时，优化方案较原始方案动作时间缩短了1.45ms；当短路电流为15kA时，则动作时间缩短0.42ms。
为了验证计算结果，制作了一台优化样机和原样机作实验比较，考虑到直接测量脱扣器动作时间比较困难，这里采用测量操作机构主轴启动时间的间接方法，把角位移传感器装在断路器主轴上，在振荡回路上分别通过4kA、8kA、10kA和15kA 4种短路电流，测量原方案和优化方案的操作机构主轴启动时间，即短路电流呈现到主轴开始旋转的时间间隔，这里把它称为t′，这一时间包括磁脱扣器动作时间、脱扣装置脱扣时间和操作机构由四连杆变成五连杆的时间，考虑到优化设计对后两个时间影响很小，所以近似可认为原方案的时间间隔to′rg和新方案的间隔t′opt之差，即为优化后脱扣器缩短的时间，图4-31显示当短路电流为4kA时，原方案和优化样机测得的电流和主轴转角θw波形，表4-8列出了不同短路电流下的t′org、t′opt，实验获得的优化方案较原方案缩短时间（Δt′）exp和计算获得的缩短时间（Δt′）cal，后两者比较接近，间接说明优化计算有一定准确性。
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
改进设计：小规格拍合式脱扣器的优化详细阅读
图4-39 几种不同磁极结构的拍合式脱扣器图4-40 5种不同磁极结构的拍合式脱扣器静态吸力特性的对比表4-11 5种方案的衔铁转动惯量和脱扣电流的关系图4-41 方案a和方案e的保护特性比较由以上分析可知，改变磁极结构对降低脱扣电流的作用不大，为了增加铁轭对衔铁的电磁吸力，也可以设法改变载流导体的绕线方式，使励磁增加，吸力矩也会相应地增加，同时不改变衔铁的转动惯量和反力，从而能够达到减小脱扣电流的目的。......
2023-06-15
-
电磁脱扣器系列化的设计方案详细阅读
图4-43 增加励磁结构与原方案图4-42a的保护特性比较本节通过优化设计方法实现了一壳架电流为250A的塑壳断路器用脱扣器弹簧参数的系列化设计，共有8个脱扣器电流等级：100A、125A、140A、160A、180A、200A、225A和250A。表4-12给出了200A和250A两个电流等级时脱扣器动作情况的部分仿真结果。......
2023-06-15
-
合理选择刀具几何参数详细阅读
75°强力车刀在几何参数的选择上，充分考虑了强力车削的特点，适应了机床、工件的要求，并满足加工需要，体现出一定的先进性。而较大的κr使径向力减小，避免引起振动，为使用大前角刀具提供了条件。75°强力车刀合理选择了几何参数，使刀具具有“锐字当先，锐中求固”之特点，很好地发挥出刀具的切削能力。半精车时刀具几何参数的选择就不再赘述，表4－9所示为刀具几何角度。......
2023-07-01
- 详细阅读
-
如何优化控制器参数的整定方案详细阅读
采用分离定理大大地简化了ADRC控制器的参数的整定难度。ESO的三个参数β01、β02和β03直接决定着ESO的性能，从而影响着整个控制器设计的好坏，一般首先调节的是最为重要的参数β03，它的取值越大，越能降低系统的滞后性，然而当大到一定限度时，会造成系统的振荡。速度因子r影响着控制量的增益，可根据实际的输出情况进行调整。另外两个参数的整定过程类似于比例微分控制的参数整定方法。......
2023-06-24
- 详细阅读
-
温度传感器和参数测试优化策略详细阅读
按被测介质与测温传感器是否接触，温度测试可分为接触式和非接触式两大类。1）接触式测温方法是基于热平衡原理，其特点是测温传感器直接与被测对象相接触，两者之间进行充分的热交换，最后达到热平衡，这时测温传感器的某一物理参数的量值就代表了被测对象的温度值。主要有全辐射高温计、红外温度传感器、比色高温计和射流温度传感器等，在此不做详细介绍。......
2023-06-28
相关推荐