断路器操作机构的疲劳问题主要是由闭合与分断过程中的动态应力应变引起，因此对断路器操作机构疲劳寿命评估的前提是分合闸过程中零部件动态应力应变的准确计算。动态应力应变的计算基于柔性体的瞬态动力学分析，瞬态动力学分析是用于确定结构在承受任意随时间变化的载荷时的动力学响应的一种方法。常用的瞬态动力学求解方法包括：完全法、缩减法、模态叠加法，本章中柔性体应力应变的计算使用模态叠加法。......
2023-06-15
动态特性计算的方法与实现
【摘要】：电磁系统的动态特性的计算必须和电路方程及动铁心运动方程结合起来，同时还要使用电磁机构静态吸力特性。图4-19 螺管式磁脱扣器保护特性的计算采用拍合式脱扣器相同的实验方法，对额定电流为63A螺管式脱扣器样机进行10次测量，测得的平均脱扣时间为6.0ms，然后用本章采用的方法进行计算，得到的脱扣时间为6.5ms，相对误差为5.8%。
电磁系统的动态特性的计算必须和电路方程及动铁心运动方程结合起来，同时还要使用电磁机构静态吸力特性。考虑单相短路情况下的电路方程，由于电磁机构动作时触头仍处于闭合位置，因此方程为
初始条件为
i|t=0=0
式中 L——线路的电感；
i——短路电流；
um——电压的峰值；
ω——电源频率；
φ——合闸相角；
R——线路电阻。
电磁机构的动作过程分为两个阶段，第一阶段从短路电流开始发生到电磁吸力克服反作用弹簧的反力作用使动铁心开始运动为止。在此过程中，动铁心一直处于静止状态，工作气隙固定为最大工作气隙，此时，应满足
Fδ+mg≤Ff
式中 Fδ——电磁吸力；
mg——动铁心的重力；
Ff——负载反力。
一旦电磁吸力足够大，使铁心开始吸合，则进入第二阶段。第二阶段从动铁心被吸合开始加速运动到动铁心与极靴之间的距离达到最小工作气隙为止。在此过程中对动铁心可写出如下运动方程：
求解上式的初始条件为
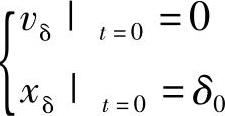
式中 m——动铁心的质量；
v——动铁心的运动速度；
Fδ——电磁吸力；
Ff——负载反力；
x——动铁心运动时的行程；
δ0——工作气隙的最大值。
用四阶龙格—库塔法联立求解方程（4-13）和（4-14），即可得电流i、电磁吸力F、动铁心速度v和行程x与时间t的关系，在每一次迭代中，吸力从脱扣器静态吸力特性曲线中通过二元二次插值获得，反力特性由用户在输入初始计算数据时输入。
对一额定电流为63A螺管式脱扣器，用上述方法计算其保护特性，线圈匝数为2匝，反力弹簧的初始预压力为0.5N，弹簧刚度为100N/m，功率因数取0.9，合闸相角取0°。开始让预期电流为一小值，若输入不能使脱扣器动作，按一定步长逐步增加预期电流值直至动铁心开始动作，计算得出这一电流为615A，这一电流为脱扣器最小动作电流，即脱扣电流。然后逐步增加短路预期电流值，计算出它的脱扣时间，从而得到它的保护特性，即预期电流和脱扣时间的关系，如图4-19所示。从图中可以看出，脱扣器的触动时间和脱扣时间都随预期电流增大而减小，并且当电流增加到一定值时，两个时间变化越来越小。
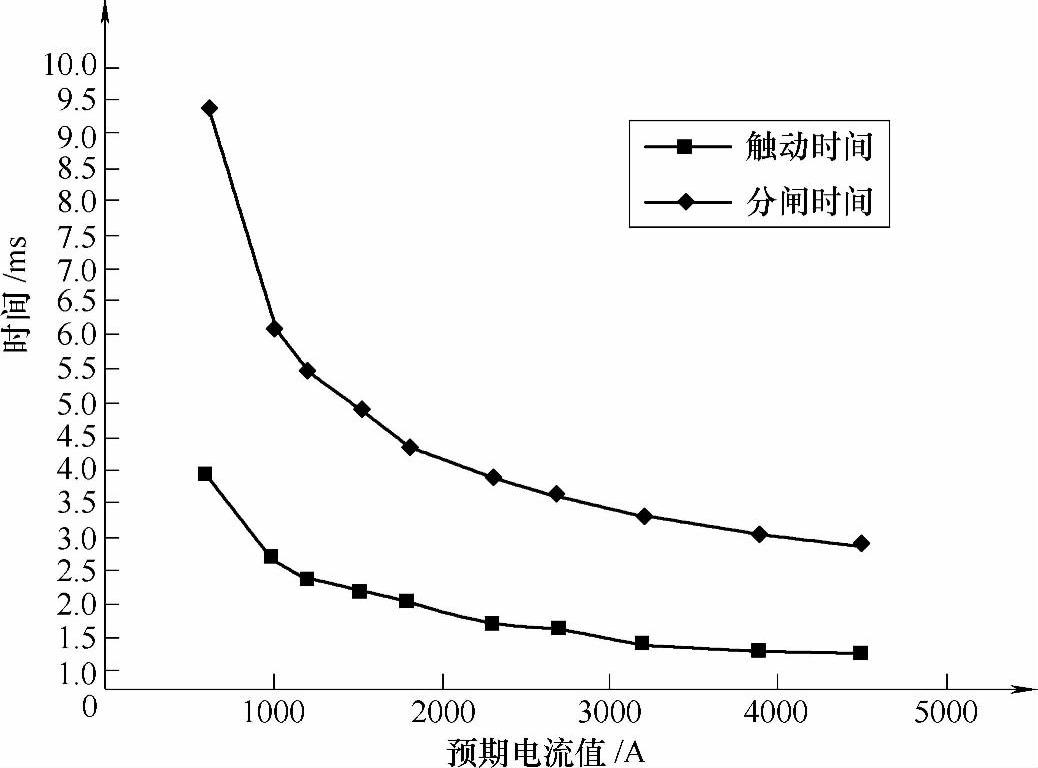
图4-19 螺管式磁脱扣器保护特性的计算
采用拍合式脱扣器相同的实验方法，对额定电流为63A螺管式脱扣器样机进行10次测量，测得的平均脱扣时间为6.0ms，然后用本章采用的方法进行计算，得到的脱扣时间为6.5ms，相对误差为5.8%。
对上述样机，在其他参数不变条件下，改变其线圈匝数，用上述方法分别求得脱扣电流和开断1000A电流的脱扣动作时间见表4-4所示，由表中数据可以看出随着线圈匝数的增加，脱扣电流减小，这说明对额定电流小的脱扣器，可通过增加线圈匝数未使脱扣器达到设定的脱扣电流要求。由表中数据还可看出，当开断1000A电流时，脱扣器动作时间也随匝数的增加而减小，这对提升断路器的开断性能有利，这也是为什么小规格脱扣器常采用螺管式的原因。
表4-4 线圈匝数与脱扣电流及动作时间的关系
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
分析EPC系统的动态特性详细阅读
由系统的传递函数框图可得EPC系统的开环传递函数为式中 k——开环放大系数，。将算得的ωh、ξh、k代入式，可据此画出EPC系统的开环伯德图。图12-18 改造前后CP机组EPC系统的开环伯德图由图12-18可得系统的性能指标为：①穿越频率：ωc=2.4Hz；②幅值裕量：h=16dB；③相位裕度：γ=75°。可见实测值和理论分析值比较接近，说明上面建立的EPC系统的数学模型和确定的参数是正确的，是可以作为预测改造后系统性能的依据的。......
2023-06-15
-
脱扣器保护特性计算方法详细阅读
表4-1示出了研究对象磁脱扣器动态特性计算的参数，为与实验结果对比。图4-10 脱扣器动作时间实验值与计算值对比表4-2 脱扣器动作时间实验值与计算值对比需要说明的是，式（4-4）为磁脱扣器动特性计算的通用方程，式中的衔铁转动惯量的求取，可利用ANSYS有限元软件来计算，为说明方法，取一平板形衔铁如图4-11所示。......
2023-06-15
-
直流电弧的动态伏安特性分析详细阅读
直流电弧的静态伏安特性是在电弧达到其稳定燃烧状态下得到的。综上所述，在电弧的弧长及电弧散热条件等外界因素不变的情况下，直流电弧的静态伏安特性只有一条，而其动态伏安特性却随着电弧电流Ih变化速度的不同，可能有无数条。......
2023-06-30
-
逆变式弧焊电源动态特性控制方法及原理详细阅读
在逆变式弧焊电源可以采用积分、微分和比较放大等电子控制电路，进行电源动特性控制和波形控制以及其他方式的控制。图6-35所示是某逆变式CO2焊接电源特性控制电路原理图。不同特性的切换是在CO2焊接过程中自动完成的，其切换过程的控制就是动特性控制。此时电压反馈信号Ufu为最大值，平特性控制电路输出最小值，VD2承受反压而截止。单独采用PI环节来实现电弧恒压控制，焊接过程稳定性仍然不能令人满意。......
2023-06-30
-
计算弧后介质恢复特性方法优化详细阅读
假设零后的介质恢复为自由恢复，不考虑电路参数的影响，令计算模型中的源项为零。最终得到如下结果：以上是SF6断路器灭弧室近区故障开断能力数值计算过程。这样，断路器端子短路故障开断能力可以用弧后介质恢复强度来表示。......
2023-07-02
-
动态拉伸计算结果的分析与优化详细阅读
然而，随着颗粒体积分数的增大，炸药的脆性增加，更容易发生拉伸破坏。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。图8－35三种不同颗粒体积分数和颗粒分布细观结构模型的应力－应变曲线图8－36～图8－38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。从三种模型的计算结果可以发现，动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。......
2023-06-27
-
SSDC对直流动态响应特性的影响分析详细阅读
为了考查直流控制系统增加SSDC模块后对直流动态响应性能的影响，本节进行了系统全接线运行方式下的直流电流参考值和直流功率参考值的阶跃动态响应特性的仿真和分析。在呼辽直流输电系统引起的伊敏电厂次同步振荡分析的电磁暂态仿真模型上进行了上述的SSDC对直流动态响应性能的仿真，状态量的阶跃响应如图7-80～图7-87所示。表7-8和表7-9给出了直流控制系统在投入与不投SSDC模块时，HVDC的直流电流、直流功率的阶跃动态响应的主要性能指标。......
2023-06-22
相关推荐