θmax从0.3054rad减小到0.2181rad,幅度为28.6%,脱扣电流则从1500A减小到1240A,幅度为17.3%;由图4-14,θ0从0.96rad减小到0.436rad,幅度为54.6%,脱扣电流则从1500A减小到890A,幅度为,由此可见改变同样大小的脱扣电流,调节θmax的方式所需的调节量比调节θ0的方式更大,并且从表4-3中还可看到脱扣电流随θ0的变化是非线性的。......
2023-06-15
结合静态特性计算得到的数据网格,磁脱扣器的动态特性,即保护特性,可以通过求解下面的方程组得到:
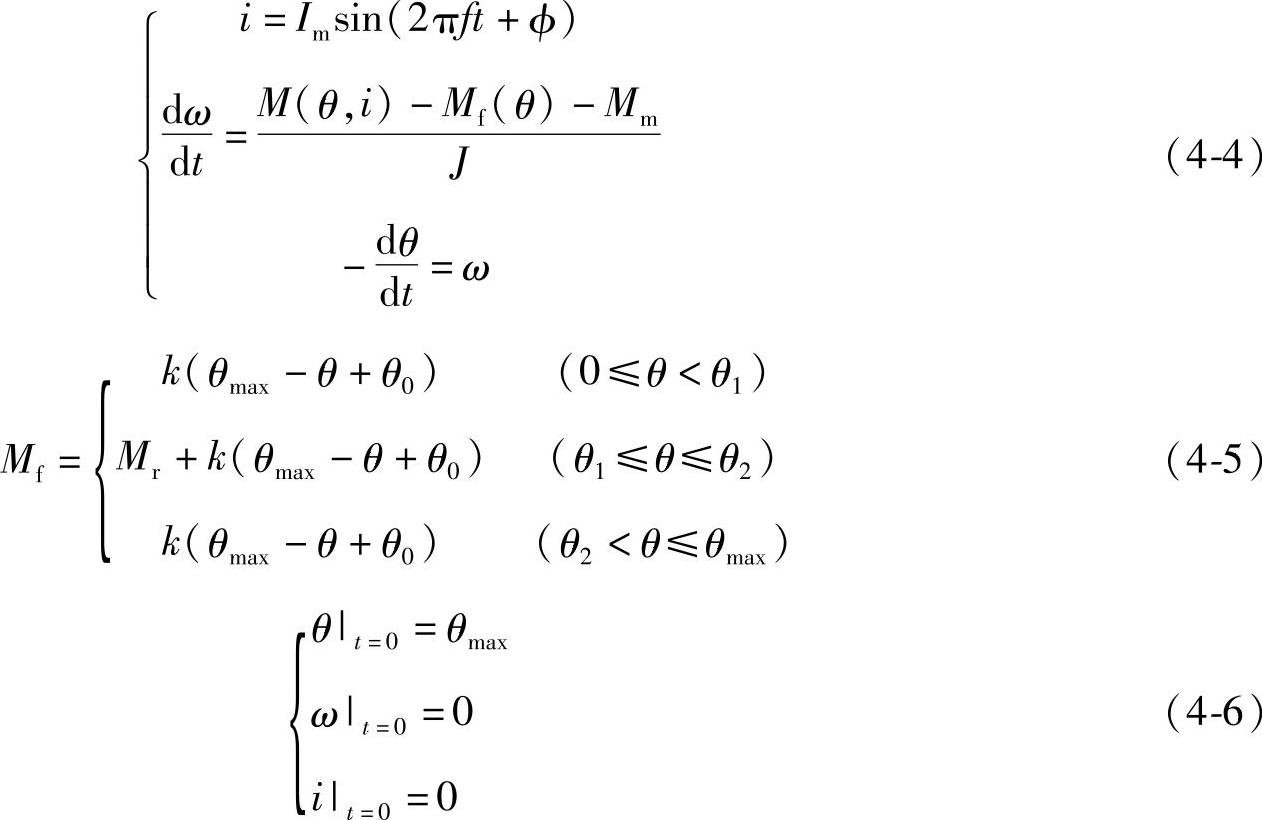
式中 θ——衔铁与铁轭夹角(工作气隙);
i——激磁电流;
φ——短路合闸相角;
Im——电流幅值;
J——动铁心转动惯量;
ω——动铁心角速度;
Mm——摩擦力矩;
M——吸力矩;
Mf——反力矩;
k——反力弹簧平均弹性系数;
θ0——反力弹簧初始拉伸(压缩)角度;
Mr——平均脱扣力矩。
Mf包括两部分:反力弹簧反力和脱扣力,其中脱扣力的作用行程很短,仅在θ1≤θ≤θ2时起作用:
θ2-θ1<<θmax-θ2 (4-7)
图4-7为反力示意图。
用四阶龙格-库塔法求解方程(4-4)时,要解决用数据网格表示的非线性函数M=f(θ,i)与其他方程联立求解的问题,这里采用第2章2.3.3节的二元插值算法,当某一瞬间t,在已知转角θ和电流i条件下求得该瞬间的衔铁转矩,以进行下一步迭代。

图4-7 磁脱扣器反力示意图
磁脱扣器在短路电流作用下的动作过程分为两个阶段,第一阶段为电磁铁触动过程,是从短路电流发生到衔铁开始动作,这一阶段衔铁不会动作,直到吸力矩大于反力矩,而θ=θmax,计算中仅求解式(4-4)中的第一个方程(电路瞬态方程);第二阶段为脱扣器衔铁运动过程,从衔铁开始运动到其带动脱扣杆并使机构脱扣为止,这一阶段的计算就是联立(4-4)中的三个方程用四阶龙格-库塔法进行离散求解,过程中所需吸力和磁链值仍由对静态数据网格二次插值得到。衔铁转动过程中的摩擦阻力主要在转轴处,力矩很小,计算中忽略不计。
表4-1示出了研究对象磁脱扣器动态特性计算的参数,为与实验结果对比。
表4-1 磁脱扣器动态特性计算参数

图4-8示出了该电磁脱扣器在1500A短路电流下的动态特性曲线。脱扣器动作时间的测量原理如图4-9所示。
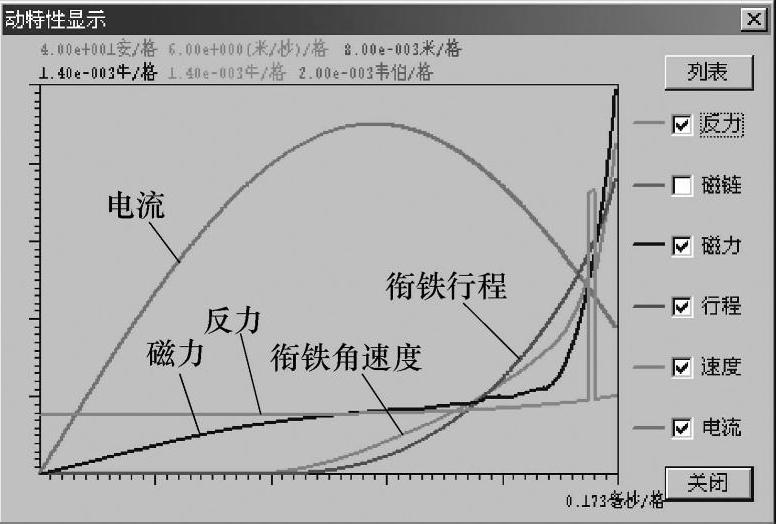
图4-8 1500A短路电流下电磁脱扣器动态特性曲线
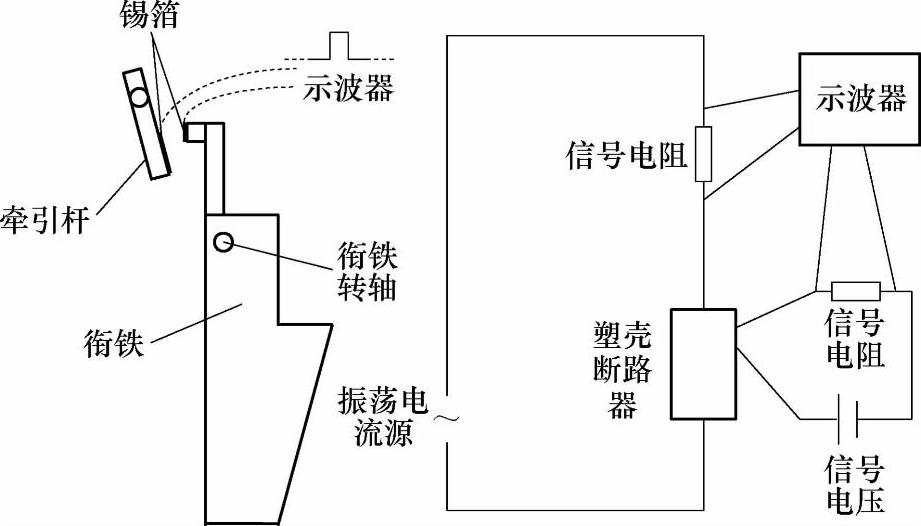
图4-9 脱扣器动作时间测量原理图
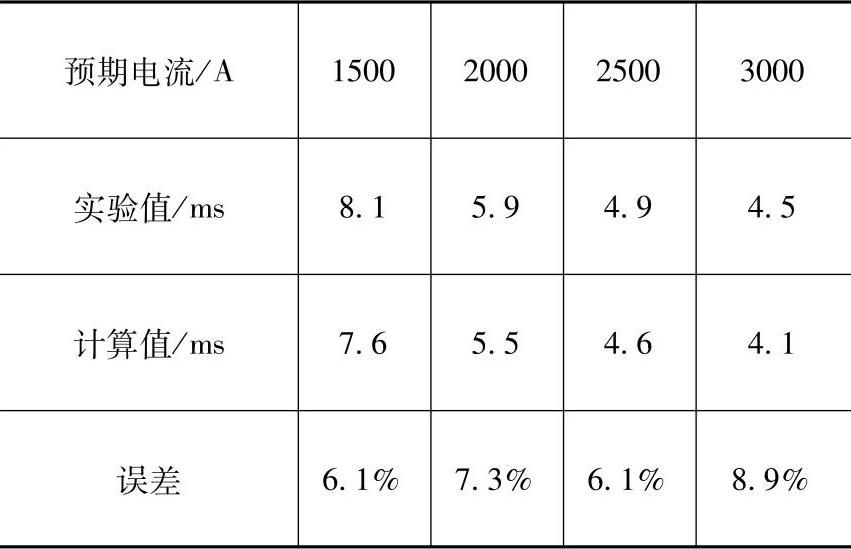
短路电流到来后,脱扣器吸力克服反力开始运动,当衔铁打到牵引杆上时,粘在上面的极薄的锡箔相接触,外部测量电路接通,示波器接收到一个电压上升沿信号,记录短路电流起始点到该上升沿信号之间的时间差作为测量值,但此时并未脱扣,衔铁还要转动一段角度才能带动牵引杆脱扣。实验中,测量值小于脱扣时间,衔铁转角为θmax-θt,相应地与实验对比的计算值也取同样的行程(见图4-7),实验值与计算值的对比曲线见图4-10和表4-2。
实验验证表明:计算值相对于试验值的误差不超过9%。
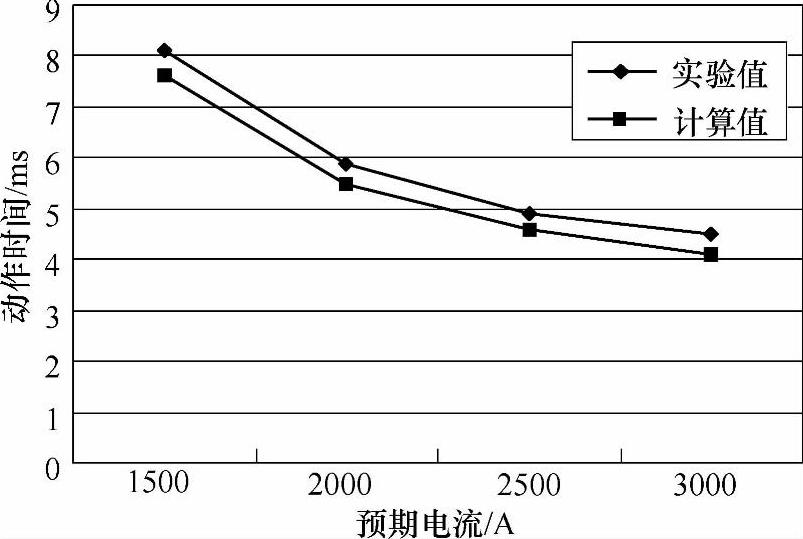
图4-10 脱扣器动作时间实验值与计算值对比
表4-2 脱扣器动作时间实验值与计算值对比
需要说明的是,式(4-4)为磁脱扣器动特性计算的通用方程,式中的衔铁转动惯量的求取,可利用ANSYS有限元软件来计算,为说明方法,取一平板形衔铁如图4-11所示。
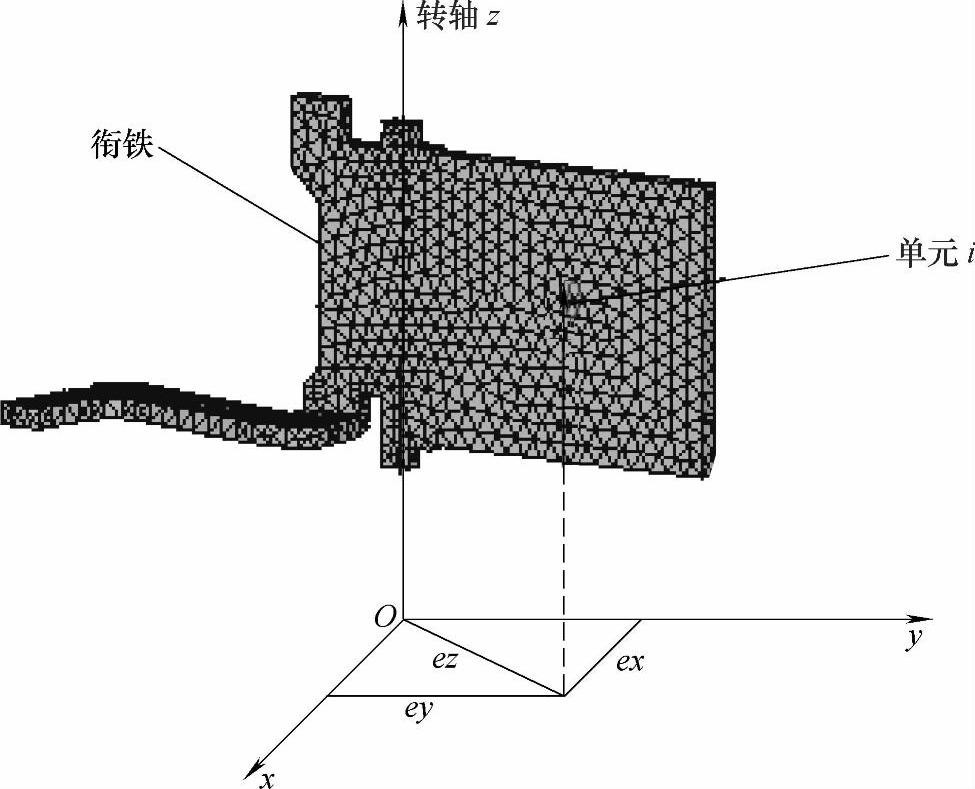
图4-11 衔铁转动惯量的求取示意图
图4-11中取衔铁上的任意一个剖分单元i,设此单元的质量为mi,体积为vi,它对转轴z轴的转动惯量为Ji,则有
Ji=mi×ez2=viρ×(ex2+ey2) (4-8)
式中 ρ——衔铁的密度,对铁其值为7850kg/m3。
设衔铁总的剖分单元数为N,则它对其转轴z轴的转动惯量J满足:
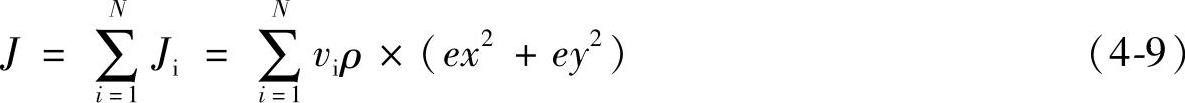
运用ANSYS有限元软件来计算衔铁的转动惯量的具体过程如下:
1)建立局部参考坐标系,使其z轴与衔铁的转轴重合。
2)因为不涉及场量的计算,可以任取一单元类型将衔铁剖分,考虑提高计算的精确性,可以剖得密一些。
3)运用*get,N,elem,,count命令,来统计衔铁单元的总数N。
4)令衔铁初始转动惯量J为零,然后使用一个简单的循环语句来求整个衔铁的转动惯量J:
*do,i,1,N !开始循环,变量i从1增至N为止
*get,ev,elem,i,volu !获取单元i的体积存于变量ev中
*get,ex,elem,i,cent,x !获取单元i的x坐标
*get,ey,elem,i,cent,y !获取单元i的y坐标
J=J+7850*ev*(ex*ex+ey*ey) !计算转动惯量
*enddo !结束循环
经过上面步骤的计算,可求得衔铁转动惯量。
有关低压断路器的建模仿真技术的文章

θmax从0.3054rad减小到0.2181rad,幅度为28.6%,脱扣电流则从1500A减小到1240A,幅度为17.3%;由图4-14,θ0从0.96rad减小到0.436rad,幅度为54.6%,脱扣电流则从1500A减小到890A,幅度为,由此可见改变同样大小的脱扣电流,调节θmax的方式所需的调节量比调节θ0的方式更大,并且从表4-3中还可看到脱扣电流随θ0的变化是非线性的。......
2023-06-15

对低压断路器的温度场仿真,首先应进行导体部分的电流场计算,求出其电流密度分布才能准确计算热源。低压断路器的热源主要是导电部分的焦耳损耗,其中包括导电排、热脱扣器和磁脱扣器,触头和出线端,以及国家标准和IEC标准中规定的温升实验中的连接导体,其中触头和出线端连接处的接触电阻对热计算的准确性影响较大,而连接导体的发热和散热也是一个需要特殊处理的问题。......
2023-06-15

磁脱扣器的静态场分析采用三维有限元方法,借助ANSYS有限元分析软件进行,包括载流导体内的电流场分析和脱扣器的磁场分析。脱扣器的三维磁场计算完毕后,与载流导体匝链的磁链ψ采用式(4-1)进行计算。图4-4 磁脱扣器载流导体电流密度分布在有限元分析中,模型的剖分对计算结果的精度有至关重要的影响,若剖分不合理,往往会造成很大的误差,甚至可达20%以上。......
2023-06-15

系统可进行塑壳断路器的热脱扣器冷态动作特性的计算。图5-16为通过仿真获得的断路器热脱扣器冷态动作特性曲线,计算结果与实验结果的对比如图5-17所示。这是因为,当过电流倍数大时,由于热脱扣器动作快,热量还来不及散出,只需考虑双金属片的热特性,断路器内部的其他部件的吸热和散热对双金属片温升的影响很小。当过电流倍数小时,热脱扣器动作时间长,热交换可充分进行。......
2023-06-15

与计算继电器,电磁弹射装置,电磁操动机构等装置中的电磁力不同,脱扣器的载荷为短路电流,可视为电流源,动铁心运动产生的反电势可以近似忽略。表4-5 碟片弹簧几何参数基于上述静态计算结果,可以求解该脱扣器的动态特性。利用Fmag和Fspr加载脱扣器多体动力学模型,考虑重力,忽略摩擦力,求解牛顿欧拉微分方程,可以得到脱扣器动态特性曲线,如图4-24所示,其中Ipeak为短路电流峰值。图4-23 碟片弹簧组特性曲线图4-24 脱扣器动态特性曲线......
2023-06-15

利用上述仿真方法,计算不同dc和L0组合情况下的脱扣电流整定值,可以得到该脱扣器的脱扣电流调节特性曲线。图4-25为方案1的脱扣电流调节特性曲线。表4-6与表4-7对比了上述两种方案的调节特性参数。方案1中各档的皮尔逊相关系数都比方案2中的皮尔逊相关系数更接近于1,故方案1线性度较好。......
2023-06-15

作为短路保护的电磁脱扣器对断路器的短路开断过程有重要作用,它的动作时间越短,越有利于提高短路开断性能,对塑壳断路器来说,更有利于达到操作机构动作与触头斥开过程的合理配合,防止动触头斥开后的跌落现象。所以实现电磁脱扣器的优化设计,一般可取动作时间最短作为优化的目标,而把几何尺寸作为设计变量。......
2023-06-15

直接起动器的选用,除应考虑保护特性外,其他参数的确定原则和接触器相同。目前,国内常用的直接起动器产品主要有QC0、QC8、QC10和QC12系列。此外还有QC71—10型起动器,可控制3台电动机的起动,实际上是3套电路的组合。MC系列电磁起动器还符合IEC92及有关船级社标准,可用于船上。......
2023-06-30
相关推荐