关键轴位置作为操作机构设计变量

2023-06-15 百科知识版权反馈

【摘要】：以图2-31中的触头主轴O1为参考点，操作机构关键轴A、B、C，O2的中心X，Y坐标为设计变量，进行设计研究。这一结论为进一步优化设计奠定了基础。以触头主轴的平均角速度最大为目标函数，设计变量在指定的范围内变化。在优化过程中，ADAMS自动调整设计变量，以获得最佳目标函数值。表2-7为考虑DV_1、DV_3、DV_6、DV_74个变量时机构的优化分析结果。以上分析结果可以作为设计五连杆型的塑壳断路器操作机构时的参考。

优化设计是ADAMS软件提供的一种复杂的分析工具。优化分析问题可归结为：在满足各种设计条件和在指定的变量变化范围内，通过自动地选择设计变量，由分析程序求取目标函数的最大值或最小值。优化的目标函数是一个数值表达式，可以表示质量、效率、总材料成本、运行时间和所需的能量等。可以选择在优化分析中是求取最大值还是最小值。设计变量可以是构件的质量、几何尺寸和力的大小等。优化分析中的约束是有条件的，这些边界条件能够直接或间接地消除无法接受的计算结果。

ADAMS软件内嵌的优化算法有DOT优化算法，OPTDES算法，这些算法已得到了世界范围内的广泛认可，对用户而言，进行优化设计只需要确定收敛容差和最大迭代次数即可。此外，用户还可自编写优化算法嵌入到ADAMS软件中。断路器机构优化设计所选用的优化算法是OPTDES-GRG（Generalized Reduced Gradient）算法。

以图2-31中的触头主轴O₁为参考点，操作机构关键轴A、B、C，O₂的中心X，Y坐标为设计变量，进行设计研究。设置设计变量的变化范围见表2-6，观察每个变量对平均分断角速度的影响。

表2-6 轴的位置设计研究结果

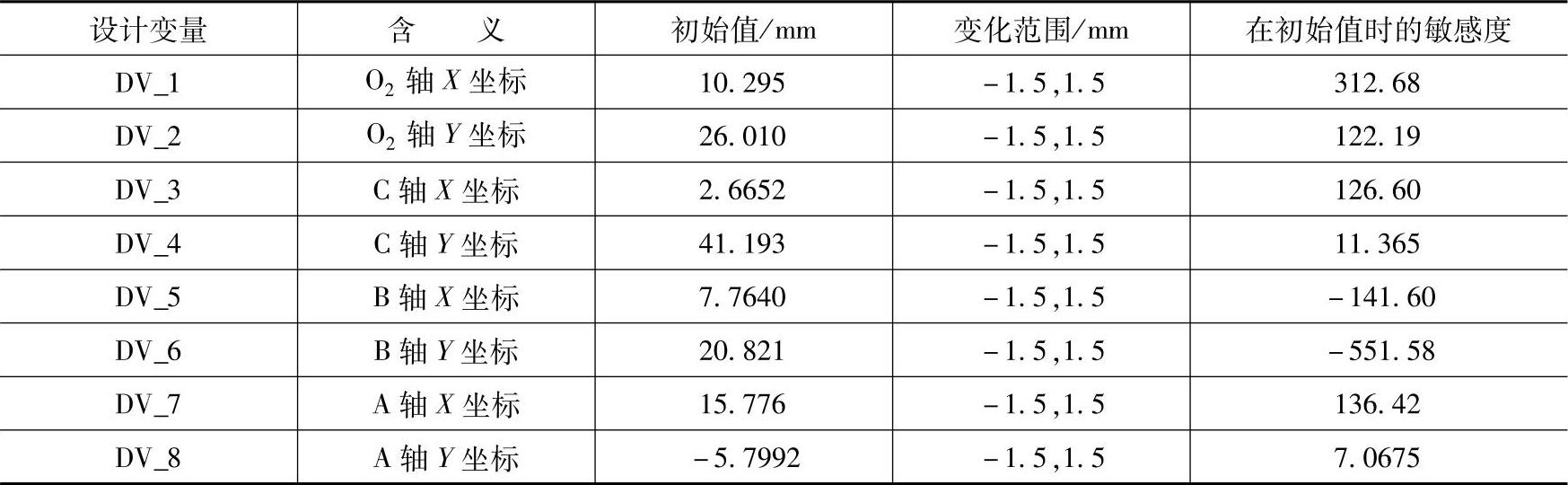
以轴O₂的X坐标变化为例，当轴O₂离坐标原点O₁最近时，触头转轴达到最大角度所需时间为10.73ms，当其离坐标原点O₁最远时，到达触头主轴最大角度所需时间为8.89ms。

从表2-6中可以看出，变量DV_1、DV_3、DV_6、DV_7的敏感度相对较大，即轴O₂、C、A中心的X轴坐标和轴B中心的Y轴坐标对分断过程中动触头主轴平均角速度影响较大。这一结论为进一步优化设计奠定了基础。

优化分析可以考虑多个设计变量同时发生变化时对样机性能的影响，并给出多个变量的最优配合，即使目标函数达到所要求的最佳值。优化分析的三个步骤如下：

1）确定最小化或最大化的目标函数。

2）选定要调整的设计变量。

3）定义必须满足的约束函数。

以触头主轴的平均角速度最大为目标函数，设计变量在指定的范围内变化。在优化过程中，ADAMS自动调整设计变量，以获得最佳目标函数值。表2-7为考虑DV_1、DV_3、DV_6、DV_74个变量时机构的优化分析结果。

表2-7 优化设计结果

从表2-7中可以看出，在考虑4个变量同时变化的情况下，经过优化设计的迭代运算，找到每个变量的最优点，使动触头主轴的运动速度从4825.22deg/s提高到5566.4deg/s，所用时间由9ms缩短到7.753ms，并能自动生成新的样机模型。在分断过程中，优化前后的动触头主轴角速度随时间变化的曲线如图2-32所示，1是优化前的角速度曲线，2是优化后的角速度曲线。以上分析结果可以作为设计五连杆型的塑壳断路器操作机构时的参考。

图2-32 优化前后的动触头主轴角速度变化

1—优化前 2—优化后

表2-8是优化前后一些仿真结果对比情况，仿真研究表明，一般需在手柄施加43N的力才能使该型号塑壳断路器合闸，机构优化后最小合闸力减小到39N，刚分速度由原来的1.15m/s提高到2.08m/s，说明了优化结果是合理可取的。

表2-8 优化前后结果对比

关键轴位置作为操作机构设计变量

相关推荐