计及电动斥力效应的断路器分断过程仿真分析

2023-06-15 百科知识版权反馈

【摘要】：图2-24 分断过程的电动斥力的计算方法图2-25是分断过程作用在动触头上的电动斥力的仿真曲线。图2-25 电动斥力的仿真曲线图2-26是计及电动斥力作用下的触头主轴角位移的仿真结果与实验结果对比，造成仿真曲线与实验曲线在最后阶段有差异的原因是没有考虑电弧气动斥力。与手动脱扣比较，由于短路情况下电动斥力的作用，提高了动触头分断速度，机构的动作时间缩短了约1ms。

对断路器分断短路电流的动态过程进行仿真，需要耦合电路、电磁场和机械运动方程进行求解，通过对ADAMS软件进行二次开发，实现了这种耦合求解的问题。

如图2-21所示，曲线1是试验短路电流波形（预期电流为10kA），曲线2是短路电流的拟合曲线，得到拟合曲线的计算公式为

I（t）=10386.51443sin（3.14t/0.00829）（2-9）

洛伦兹力是电流i和触头转角a的函数，即F_c=f（a，i）。将触头转角和电流值在其范围内各分成几段，利用ANSYS求出不同转角时的每一个电流值所对应的有限元模型的洛伦兹力，将计算得到一个二维数据表格，图2-22是不同触头转角下，洛伦兹力随电流变化的关系曲线。在动态仿真过程中，任何时刻触头转角、短路电流值下的洛伦兹力可通过数据表格中结果，运用二元插值技术求得。设触头转角a为x方向，电流值i为y方向，w为插值点对应的洛伦兹力值，对于任意给定的不是节点的插值点w（u，v），选取最靠近其的9个节点，其两个方向上的坐标分别为x_p<x_p+1<x_p+2，y_q<y_q+1<y_q+2，然后用二元三点插值公式（2-10）计算插值点（u，v）处的函数近似值w。此外，计算程序也对计算过程中可能会出现的几种边值情况进行了处理，二元三次插值计算的流程图如图2-23所示。

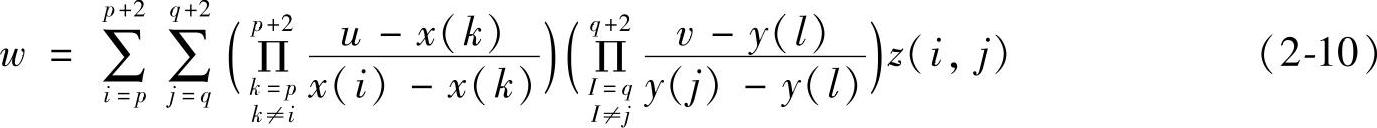
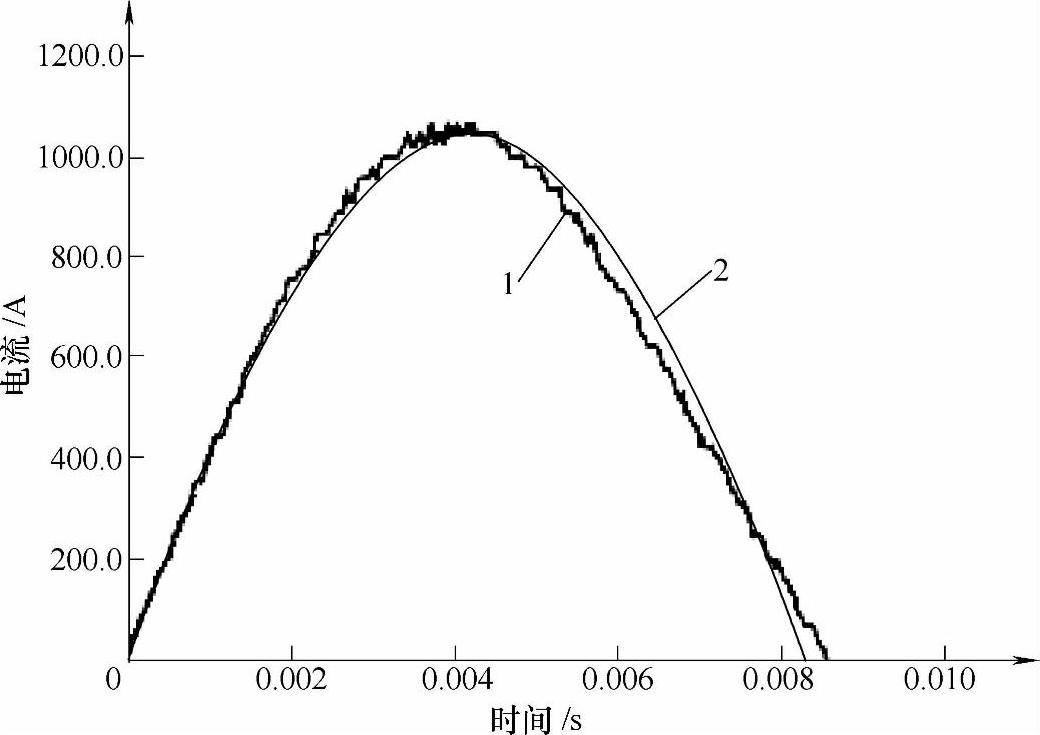
图2-21 试验短路电流波形及其拟合曲线

1—试验短路电流波形 2—短路电流的拟合曲线

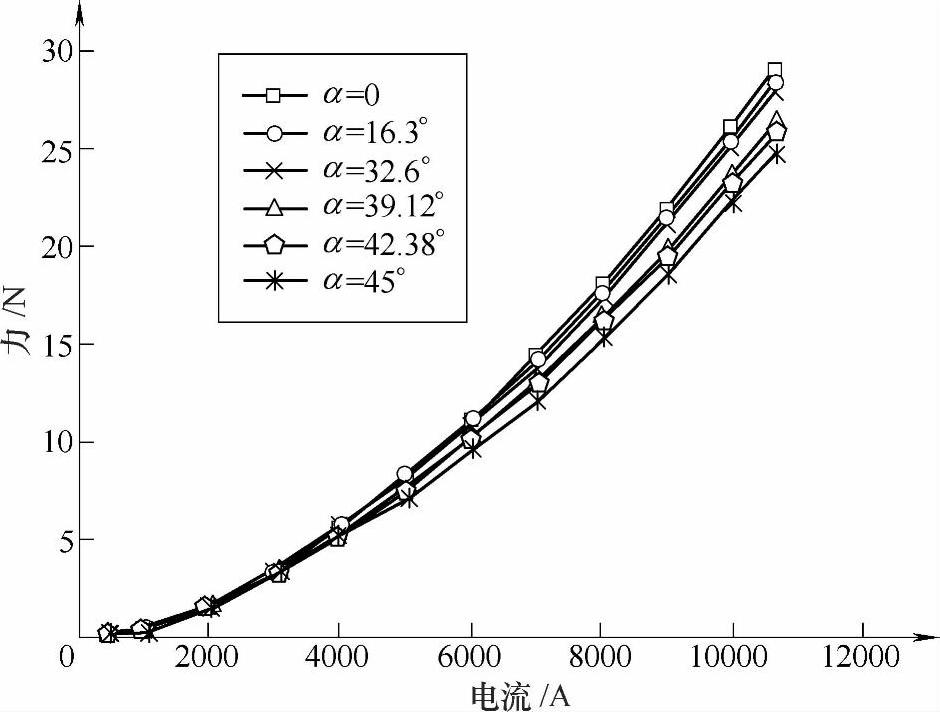
图2-22 不同触头开距下，洛伦兹力与电流的关系曲线

ADAMS软件二次接口程序主要由以下步骤完成电动斥力的计算：

1）由解析式（2-1）计算霍姆力；

2）由式（2-9）计算对应该瞬间t的电流值；

3）在已知该瞬间电流和转角条件下，采用二元三点插值方法查取洛伦兹力；

4）将以上霍姆力和洛伦兹力计算结果之和，即电动斥力通过二次接口函数返回到AD_- AMS。

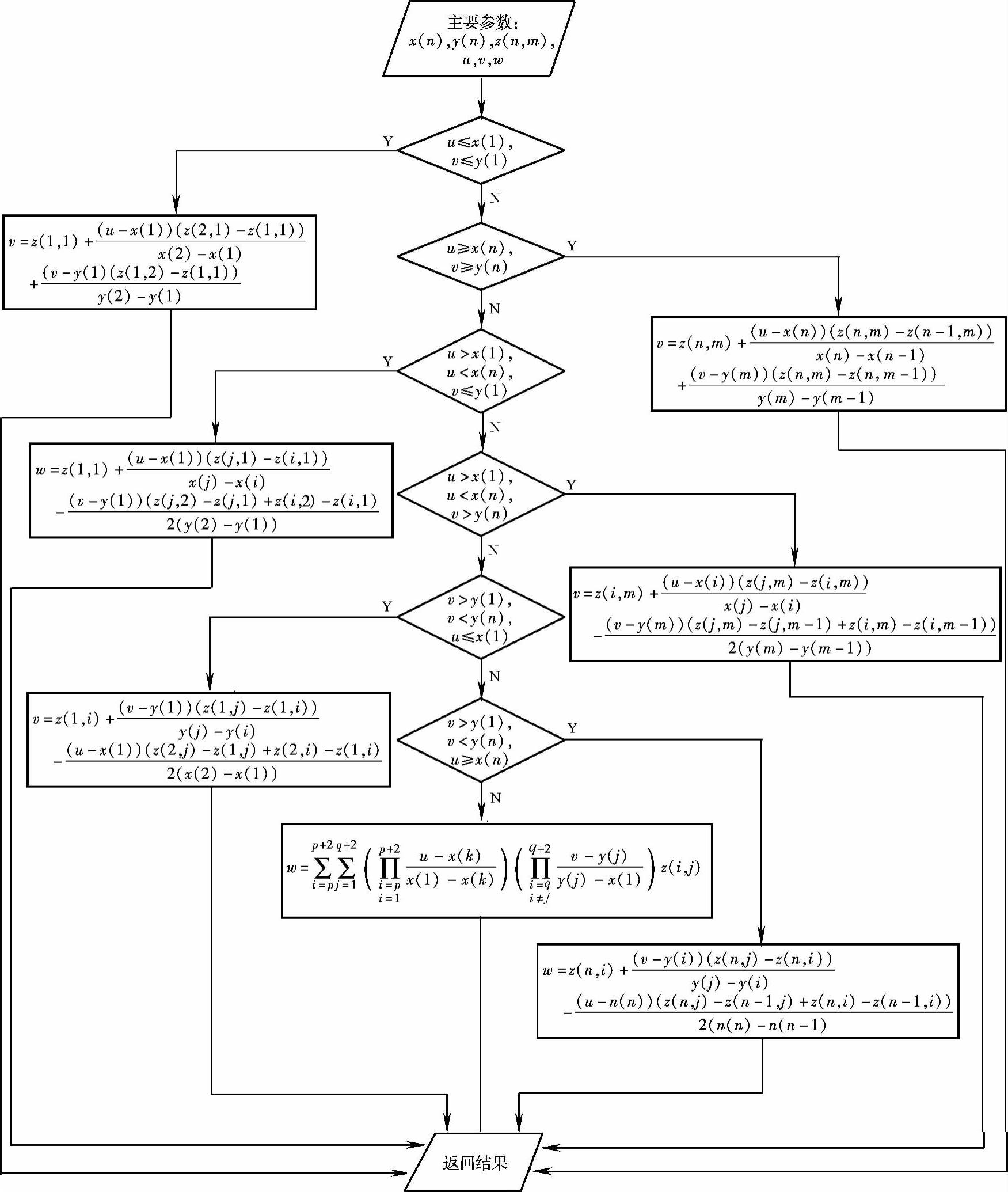
图2-23 二元三次插值计算的流程图

在机构分断过程的仿真中，可以从ADAMS软件中读到t时刻的触头转角值，通过接口程序求得一个可作为t+Δt时刻的电动斥力值，并带回到ADAMS软件中，如图2-24所示。同时，该力施加在断路器仿真模型中间相动触头中心位置上，通过这种双向不断的迭代计算，可仿真出分断短路电流的整个动态运动过程。

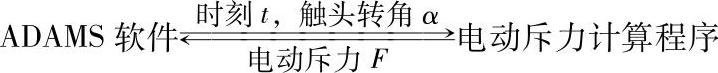
图2-24 分断过程的电动斥力的计算方法

图2-25是分断过程作用在动触头上的电动斥力的仿真曲线。造成电动斥力在t₁时刻，由A点突跳到B点是因为电动斥力克服触头扭簧，造成动静触头分离，霍姆力消失，之后洛伦兹力随短路电流发生近似正弦规律的变化。

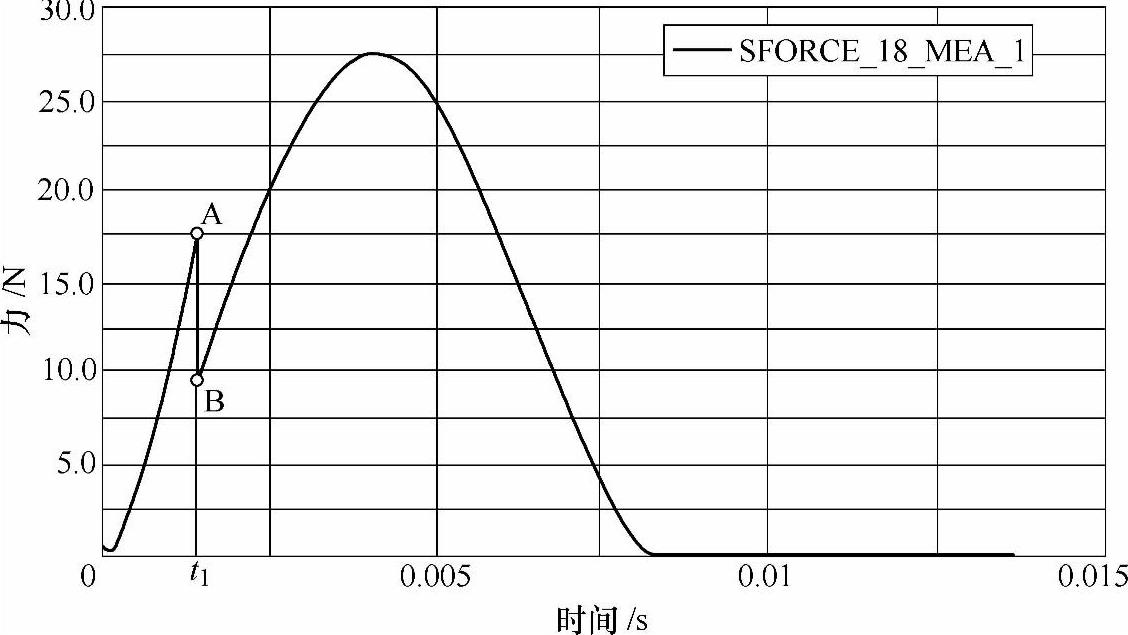
图2-25 电动斥力的仿真曲线

图2-26是计及电动斥力作用下的触头主轴角位移的仿真结果与实验结果对比，造成仿真曲线与实验曲线在最后阶段有差异的原因是没有考虑电弧气动斥力。图2-27是分断过程的触头主轴角位移和动触头角位移仿真曲线对比图。短路电流出现时刻是仿真分断过程的起点，由短路试验波形可知操作机构约在短路电流出现5ms后才开始动作，因此短路电流刚出现的一段时间内，脱扣器没有动作，所以机构没有动作，触头主轴也没有转动，主轴角位移曲线是条零值水平直线，但是随着电流的增加，当电动斥力足以克服触头预压力时，动触头被斥开一定角度。在短路电流起始阶段T_a时间内，由于霍尔姆力的消失和触头扭簧的扭矩作用，触头会发生回落现象，当脱扣器动作，机构冲过死区后，动触头将随着机构一起运动，从图2-27可清楚观察到在T_a阶段后，触头主轴角位移曲线与动触头角位移曲线重合，表明在T_a之后的动触头与机构是同步转动的如图2-28所示。与手动脱扣比较，由于短路情况下电动斥力的作用，提高了动触头分断速度，机构的动作时间缩短了约1ms。

图2-26 触头主轴角位移仿真与实验曲线的对比（预期电流为10kA）

1—实验曲线 2—仿真曲线

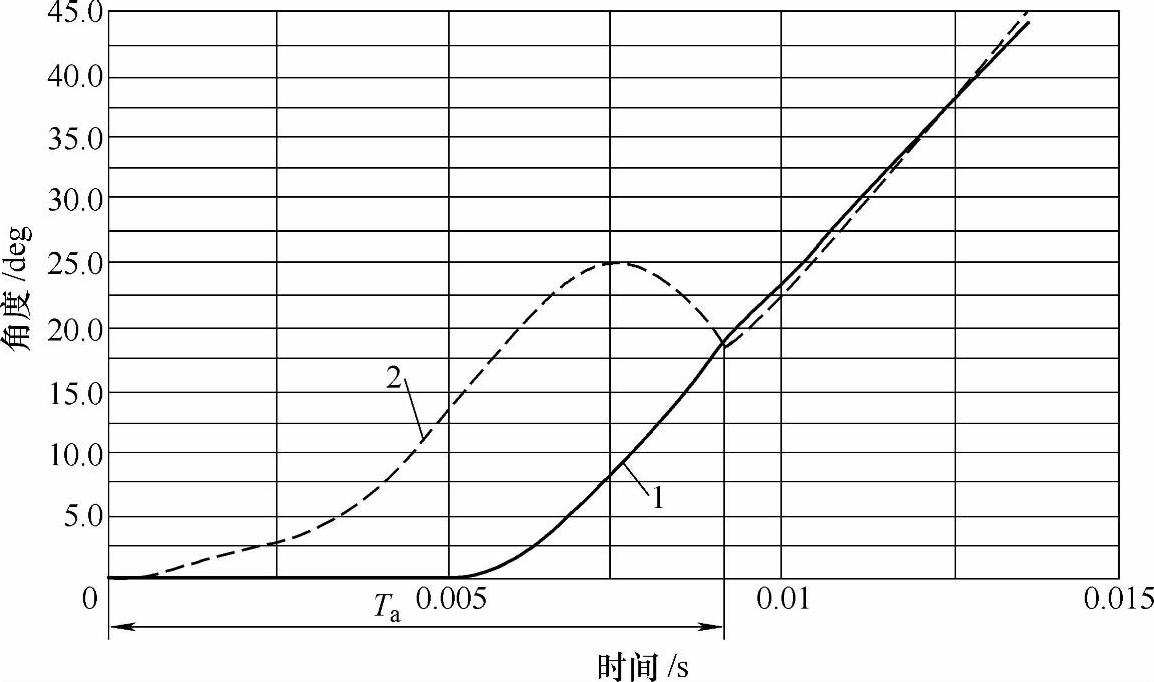
图2-27 计及电动斥力角位移的仿真曲线

1—触头主轴角位移仿真曲线 2—动触头角位移仿真曲线

如前面2.1.2节所述，计及电动斥力的开断过程仿真要采用脚本仿真，这是因为计及了电动斥力，开断过程分成两个阶段，第一阶段是跳扣不动作，动触头在电动斥力作用下与静触头分离，与此同时瞬时脱扣器在短路电流作用下，经过一定时间解开扣锁，使跳扣动作；随后进行第二阶段，第二阶段由于跳扣动作，机构主轴开始转动，带动动触头支架，当动触头支架追上动导电杆，动触头就在主轴带动下，向打开位置转动，直至开断过程结束。采用脚本仿真来实现上述开断过程，在第一阶段要在跳扣与地建立固定约束，让电动斥力去斥开动触头，经过5ms时间，瞬时脱扣器使跳扣动作，这时应解除跳扣与地的固定约束，让跳扣和机构主轴可以动作，这一过程直到开断过程结束。在ADAMS软件上实现上述脚本仿真可采用ADAMS/Solver命令集，即ACF（ADAMS/Solver Command File），具体操作：在执行菜单中选Simulate/Simulation Script/New命令，打开Create Simulation Script对话框，在下拉列表框中选取ADAMS/Solver Com_- mands，呈现的对话框中系统提示：Insert ACF Commands here：，接着输入命令，可用手动输入方式也可用系统提供的命令列表中选取，完成计及电动斥力的开断过程脚本仿真的ACF命令集如下：

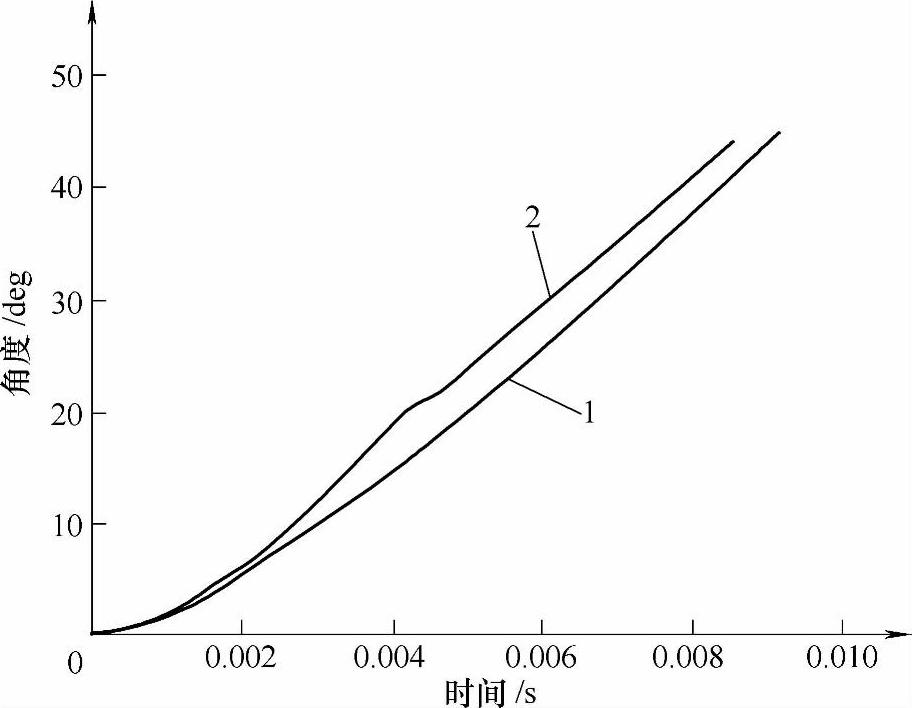
图2-28 手动脱扣与分断短路电流的触头主轴角位移曲线对比图

1—手动脱扣 2—短路脱扣（预期电流为10kA）

！Insert ACF Commands here：

SIMULATE/DYNAMIC，DURATION=5e-3，STEPS=100

DEACTIVATE/JOINT，ID=57

SIMULATE/DYNAMIC，DURATION=0.2，STEPS=300

仿真建模时，首先让跳扣对地建立一个固定约束，上述命令集中第一条为动力学仿真，DURATION为仿真持续时间，STEPS为仿真总步数，仿真持续时间取从短路开始到机构开始动作所需时间，即5ms；第二条为解除ID号为57的跳扣对地的固定约束的作用；第三条是在跳扣和主轴动作条件下进行动力学仿真，持续时间取得较长，即0.2s，是为了保证完成整个开断过程。

以上尽管只讨论了单相短路电流对机构动特性的影响，但类似方法也可引伸用于三相短路电动力的影响。

计及电动斥力效应的断路器分断过程仿真分析

相关推荐