动触头受电动斥力分析

2023-06-15 百科知识版权反馈

【摘要】：如上所述，在触头未斥开前，作用在动触头上的电动斥力包括触头间由于电流收缩产生霍姆力FH和导电回路产生的洛伦兹力FL。断路器导电回路上洛伦兹力FL一直存在至电弧熄灭，与电流的平方近似成正比关系。忽略涡流的影响，采用恒定场的方程来计算电流密度和磁通密度的分布，这样可以分三步来完成电动斥力的计算。图2-17 洛伦兹力计算流程图而对于低压断路器来说，动触头一般是在一个对转动轴的力矩M的作用下打开的，如图2-18所示。

如上所述，在触头未斥开前，作用在动触头上的电动斥力包括触头间由于电流收缩产生霍姆力F_H和导电回路产生的洛伦兹力F_L。计算电动力时，必须同时考虑以上两个力。由于洛伦兹力和霍姆力的产生机理不尽相同，在计算时需要分别考虑。

动静触头接触处具有如图2-16所示的电流-电位场，并满足如下假设：

1）接触内表面中心只有一个导电斑点，或者认为全部导电斑点集中在中心形成一个大的导电斑点；

2）接触面上的导电斑点不是一个平面而是一个超导小球，此超导小球为一个等位体。

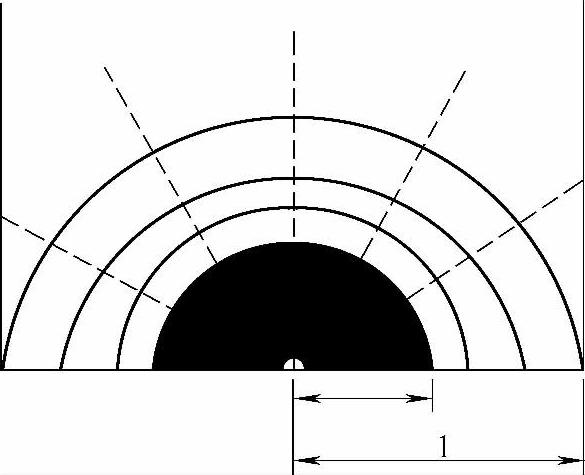
图2-16 假定的电流-电位场

令导电斑点超导小球的半径为r，圆柱形接触导体的截面半径为R，则触头间由于电流线收缩产生的电动斥力F_H满足公式：

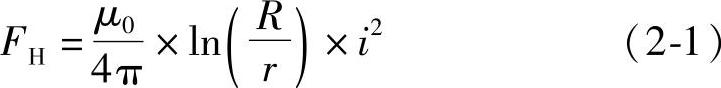
导电斑点的半径可用式（2-2）来描述：

式中 i——流经收缩区导体的电流（A）；

ξ——与触头表面接触状况有关的系数，其范围在0.3～0.6之间；

H——材料的布氏硬度（N/mm²）；

F_K——接触力（N）。

对于银钨材料AgW（50），故式2-2中H取900N/mm²；ξ取0.45；触头半径R为2.8mm；接触力F_K=18N。

由电流线收缩产生的电动力F_H只存在于动静触头保持金属接触状态的时间里，即在分断过程中接触压力F_K在不断减小。因此，在分断短路电流的过程中，F_H仅存在于超行程阶段并随着i和F_K不断变化，动静触头分开后，该力就不存在了。

断路器导电回路上洛伦兹力F_L一直存在至电弧熄灭，与电流的平方近似成正比关系。在传统的近似计算中，常把动、静导电杆看作平行导体来计算斥力，这种方法在工程实际中常因触头系统的复杂性造成很大误差，因此采用有限元分析软件ANSYS计算回路洛伦兹力，可提高计算结果的准确性，其具体计算流程如图2-17所示。忽略涡流的影响，采用恒定场的方程来计算电流密度和磁通密度的分布，这样可以分三步来完成电动斥力的计算。首先根据导电回路和导电斑点的情况进行三维电流密度分布仿真，此时仅需对导电部分进行剖分；接着，对同一个模型，将电流分布当作激励，对整个模型区域进行剖分，计算其产生的三维磁场；最后，根据式（2-3）计算出作用在每一个单元上的电动斥力F_i。

F_i=J_i×B_i （2-3）

式中 J_i——每个单元的电流体密度；

B_i——单元磁感应强度。

对于孤立触头来说，可以用式（2-4）来计算作用在触头上的电动力，也就是力密度F_i对整个触头区域V的体积分。

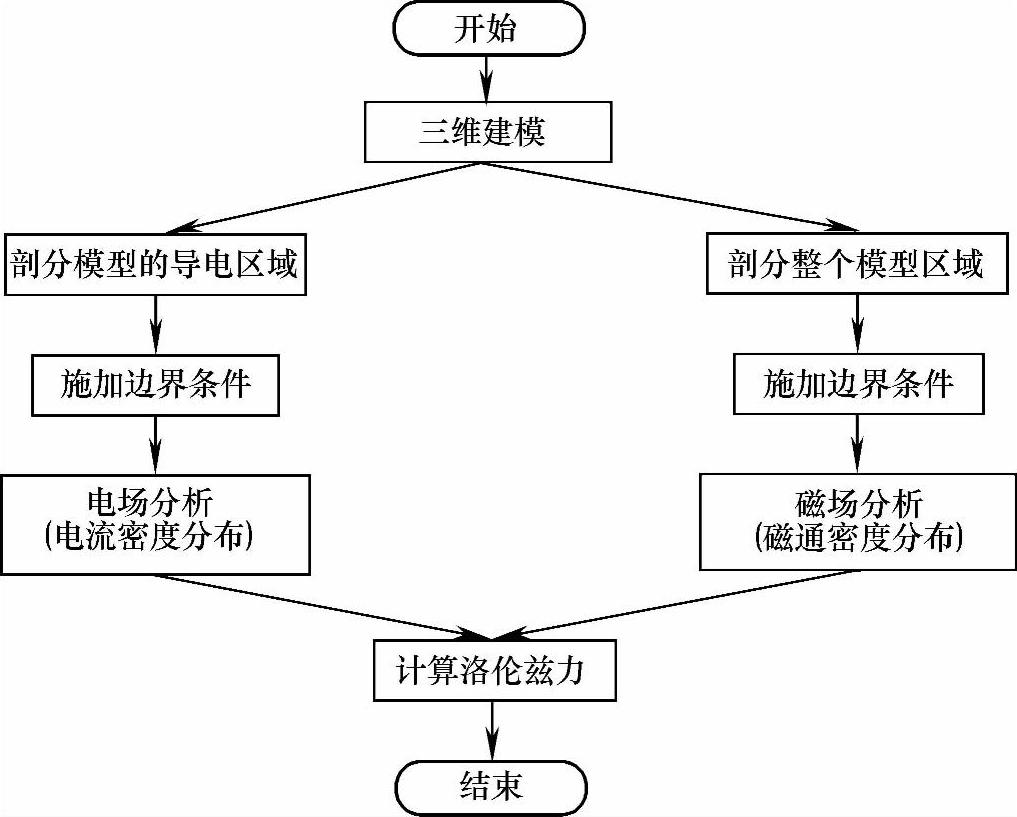
图2-17 洛伦兹力计算流程图

而对于低压断路器来说，动触头一般是在一个对转动轴的力矩M的作用下打开的，如图2-18所示。作用在其上的等效电动力可以通过式（2-5）求得。也就是说，对任何一个单元i来说，其对于转轴O的转矩M_i为d_i和力密度F_i的向量积，那么在整个动导电杆区域对M_i进行体积分运算，则可得到作用在其上相对于O的力矩，力矩除以力臂l就可以得到等效电动力。

图2-18 作用在动导电杆上的电动斥力计算示意图

在导电体区域，也就是触头导电回路中，电流密度J满足式（2-6）和式（2-7）所示的边界条件。

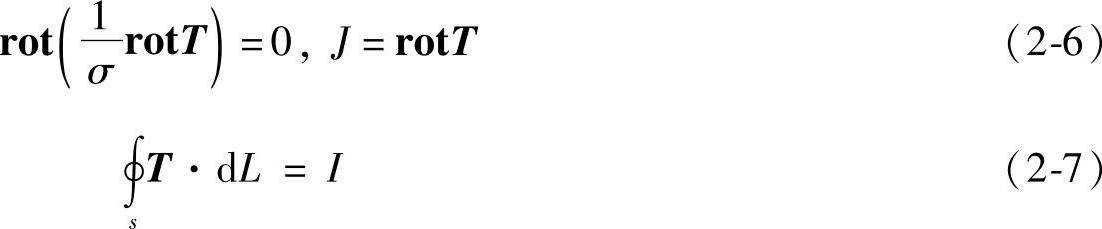
式中 σ——导体的电导率；

T——矢量电位；

I——流过导体的电流。

在得到了电流密度J的分布后，在整个场域中，根据磁通密度B和J之间的关系式（2-8）。

式中 A——矢量磁位；

μ——磁导率；即可得到B的分布。

由于模型具有对称性，因而选其一半进行计算分析。图2-19是三维模型闭合位置和打开位置时的有限元剖分图。当触头间产生电弧，动静触头间的气体被强烈加热，产生膨胀力，该力是粒子热运动对触头的撞击力，而触头间的气体受到触头的阻挡，不能迅速逸出时，该力就会产生，因此该力与触头开距和电弧能量有很大关系，很难用数学模型来描述。为简化计算，不考虑电弧气动斥力对断路器分断特性的影响，认为动静触头间的弧柱的截面积与触头截面积尺寸相等。从图2-20中可以清楚地观察到导电回路上电流密度的分布情况。本章的有限元分析都是相对于该图所示的坐标系进行的，该坐标系符合右手法则。

图2-19 三维模型有限元剖分图

a）闭合位置 b）打开位置

图2-20 电流密度分布

动触头受电动斥力分析

相关推荐